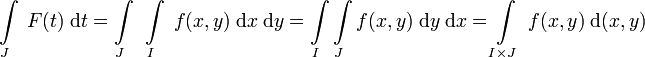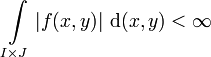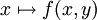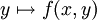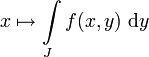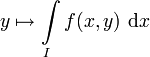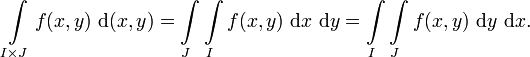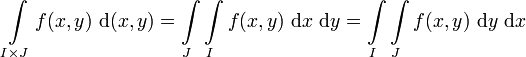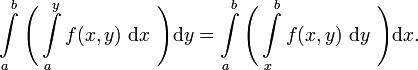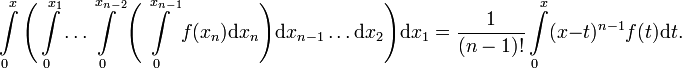Satz von Fubini-Tonelli

Der Satz von Fubini ist ein wichtiger Satz in der Integralrechnung. Er gibt an, unter welchen Bedingungen und wie man mehrdimensionale Integrale mit Hilfe von eindimensionalen Integralen ausrechnen kann. Erstmals wurde dieser Satz von Guido Fubini bewiesen.

Beschreibung

Mit Hilfe des Riemann-Integrals oder des Lebesgue-Integrals kann man die Integration von Funktionen über mehrdimensionale Gebiete definieren. Das Problem hierbei ist, dass diese Integrale über einen Grenzwert mit Hilfe einer Zerlegung des Gebiets in kleine Teile definiert sind. Diese ergibt vorderhand keine nützliche, konstruktive Methode, um solche Integrale zu berechnen. Bei eindimensionalen Integralen kann man diese Grenzwertbildung vermeiden, wenn man die Stammfunktion kennt (Hauptsatz der Differential- und Integralrechnung).

Mit Hilfe des Satzes von Fubini können nun mehrdimensionale Integrale auf eindimensionale zurückgeführt werden, welche wiederum mit Hilfe einer Stammfunktion (sofern bekannt) berechnet werden können. Dieser Trick ist in naiver Weise (vor einer exakten Definition der Integrationsrechnung) schon im 16. Jahrhundert verwendet worden – im Falle von Volumensberechnungen unter dem Prinzip von Bonaventura Cavalieri bekannt.

Satz von Fubini für das Riemann-Integral

Seien 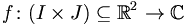$f\colon ({I \times J}) \subseteq {\mathbb{R}^2} \to \mathbb{C}$ stetig, I und J kompakte Intervalle.

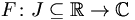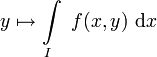Dann ist $F\colon {J} \subseteq {\mathbb{R}} \to \mathbb{C}$ mit $y \mapsto \int\limits_{I}^{}~f(x,y)~ \mathrm dx$ stetig und es gilt

$\int\limits_{J}^{}~F(t) ~ \mathrm dt = \int\limits_{J}^{}~\int\limits_{I}^{}~f(x,y)~ \mathrm dx ~ \mathrm dy = \int\limits_{I}\int\limits_{J}f(x,y)~\mathrm dy~ \mathrm dx = \int\limits_{I \times J}^{}~f(x,y) ~ \mathrm d(x,y)$

Satz von Fubini für das Lebesgue-Integral

Sei f(x,y) eine reelle messbare Funktion, die bezüglich des Produktmaßes d(x,y) integrierbar ist, d.h. es gelte

$\int\limits_{I \times J} |f(x,y)| ~ \mathrm d(x,y) < \infty \$

oder sei f eine reelle, messbare und nichtnegative Funktion, d.h. es gelte

$f(x,y) \geq 0 \; \forall\, x,y$.

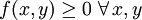Dann ist für fast alle y die Funktion

$x \mapsto f(x,y)$

und für fast alle x die Funktion

$y \mapsto f(x,y)$

integrierbar bzw. nichtnegativ. Man kann deshalb die durch Integration nach y beziehungsweise x definierten Funktionen

$x \mapsto \int\limits_{J} f(x,y) ~ \mathrm dy$

$y \mapsto \int\limits_{I} f(x,y) ~ \mathrm dx$

betrachten. Diese sind auch integrierbar bzw. nichtnegativ und es gilt

$\int\limits_{I \times J} f(x,y) ~ \mathrm d(x,y) = \int\limits_{J}^{}\int\limits_{I}^{}f(x,y)~ \mathrm dx~ \mathrm dy = \int\limits_{I}^{}\int\limits_{J}^{}f(x,y)~\mathrm dy~ \mathrm dx.$

Diese Identität gilt für alle Mengen I,J, die Kompaktheit ist nicht erforderlich.

Satz von Tonelli (auch Satz von Fubini-Tonelli)

Eine nützliche Variante dieses letzten Satzes ist der Satz von Tonelli. Hier wird die Integrierbarkeit bezüglich des Produktmaßes als Voraussetzung nicht benötigt. Es reicht, dass für | f | die iterierten Integrale existieren:

Sei f(x,y) eine reelle messbare Funktion. Falls mindestens eines der beiden iterierten Integrale

$\int\limits_{J}^{}\int\limits_{I}^{}|f(x,y)|~\mathrm dx~ \mathrm dy$,

$\int\limits_{I}^{}\int\limits_{J}^{}|f(x,y)|~ \mathrm dy~ \mathrm dx$

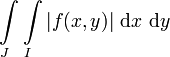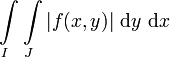
existiert, dann ist f(x,y) bezüglich des Produktmaßes integrierbar und es gilt:

$\int\limits_{I \times J} f(x,y) ~ \mathrm d(x,y) = \int\limits_{J}^{} \int\limits_{I}^{} f(x,y)~\mathrm dx~ \mathrm dy = \int\limits_{I}^{}\int\limits_{J}^{} f(x,y)~ \mathrm dy~ \mathrm dx$

Folgerung

Mithilfe des Satzes von Fubini kann man folgende Identitäten beweisen, die zum Beispiel Anwendung in der Stochastik finden.

• Sei $f:\ [a,b] \times [a,b] \longrightarrow \R$ Lebesgue-integrierbar, dann gilt:

$\int\limits_{a}^{b} \Biggl( \int\limits_{a}^{y}f(x,y)~ \mathrm dx~ \Biggr) \mathrm dy = \int\limits_{a}^{b} \Biggl( \int\limits_{x}^{b}f(x,y)~\mathrm dy~ \Biggr) \mathrm dx.$

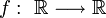• Sei $f:\ \R \longrightarrow \R$ Lebesgue-integrierbar, dann folgt induktiv:

$\int\limits_{0}^{x} \Biggl( \int\limits_{0}^{x_1} \dots \int\limits_{0}^{x_{n-2}} \Biggl( \int\limits_{0}^{x_{n-1}} f(x_n) \mathrm dx_n \Biggr) \mathrm dx_{n-1} \dots \mathrm dx_2 \Biggr) \mathrm dx_1 = \frac{1}{(n-1)!} \int\limits_{0}^{x} (x-t)^{n-1} f(t) \mathrm dt.$

Literatur

• Konrad Königsberger: Analysis 2. 5. Auflage, Springer, Berlin 2004.