Satz des Heron

Ein Dreieck mit den Seitenlängen a, b und c.

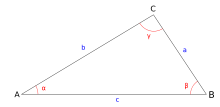
Mit dem Satz des Heron kann man den Flächeninhalt eines Dreiecks aus den drei Seitenlängen a, b und c berechnen. Der Satz ist nach dem Mathematiker Heron von Alexandria benannt.

Der Satz lautet wie folgt:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

Wobei A die Fläche und s der halbe Umfang ist, also

$s = \frac{a+b+c}{2}$

Die Formel von Heron lautet auch so:

$A = \frac{1}{4} \sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}$

Diese Formel kann als Spezialfall der Formel für den Flächeninhalt eines Sehnenvierecks angesehen werden, wenn eine Seitenlänge des Sehnenvierecks die Länge Null hat. Für den Flächeninhalt eines Sehnenvierecks gilt nämlich:

$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$

Weblinks

• Eric W. Weisstein: Satz des Heron. In: MathWorld. (englisch)
• Beweis mit Hilfe des Kosinussatzes (Deutsch) (PDF-Datei; 88 kB)
• Beweis für den Satz des Heron und seine Folgerungen (PDF-Datei; 82 kB)

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3