Schnelle Wavelet-Transformation

Die Schnelle Wavelet-Transformation ist ein effizientes Verfahren zur Berechnung einer diskreten Wavelet-Transformation. Sie kann mit der Anwendung der schnellen Fourier-Transformation zur Berechnung der Koeffizienten einer Fourier-Reihe verglichen werden.

Ein gegebenes kontinuierliches Signal f wird zunächst durch orthogonale Projektion auf einen Unterraum V _{− J} einer orthogonalen Multiskalenanalyse in eine zeitdiskrete Koeffizientenfolge s^{( − J)} umgewandelt. Je größer J ist, desto genauer ist die dadurch erzielte Approximation. In vielen Fällen ist es ausreichend, $s^{(-J)}_n:=2^{-J/2}\,f(n/2^J)$ zu setzen.

Analyse-Filterbank, g=a^-, h=b^-

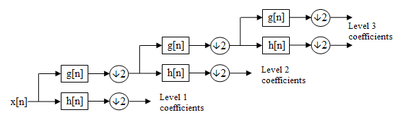
Nun wird rekursiv aus jedem Tiefpasssignal s^(k) ein neues Tiefpasssignal

$s^{(k+1)}=\frac1{\sqrt2}(\downarrow2)(a_-*s^{(k)})$

und das Bandpasssignal

$d^{(k+1)}=\frac1{\sqrt2}(\downarrow2)(b_-*s^{(k)})$

erzeugt. Zusammen bilden diese eine Analyse-Filterbank, die Operationen darin werden weiter unten erklärt.

Rekursive Anwendung einer Analyse-Filterbank

Nach M Schritten der Rekursion ergeben sich die Folgen $d^{(-J+1)},\dots,d^{(-J+M)}$ und s^{( − J + M)}. Das Ziel dieser Transformation ist, dass die d^(k) "dünn" besetzt sind und sich daher gut komprimieren lassen.

Sind die Filter a und b ausreichend frequenzselektiv, war das Ausgangssignal bandbeschränkt und wurde dem WKS-Abtasttheorem entsprechend die erste Koeffizientenfolge $s^{(-J)}_n:=2^{-J/2}\,f(n/2^J)$ gewonnen, so enthält das erste Tiefpassergebnis alle Signalbestandteile bis zur halben Nyquist-Frequenz, das Bandpassergebnis die darüberliegenden, beide Male mit einer der Bandbreite entsprechenden Abtastrate.

Analyse und Synthese

Der Fischgrätenzerlegung in der Multiskalenanalyse entspricht eine aus dem Tiefpass a und dem Bandpass b zusammengesetzte zeitdiskrete Filterbank, es wird ein zeitdiskretes Signal x aufgeteilt in ein hohes Band b ⁻ * x und ein tiefes Band a ⁻ * x (Faltung von Folgen). Danach werden beide Signale heruntergetaktet (englisch "downsampling") zu $s=(\downarrow2)(a^-*x)$ und $d=(\downarrow2)(b^-*x)$. Mit a ⁻ sei dabei die zeitinvertierte Folge $a^-=\{\dots,a_{2},a_{1},a_{0},a_{-1},a_{-2},\dots\}$ bezeichnet. Das Heruntertakten einer Folge bedeutet, dass eine neue Folge aus den Gliedern mit geradem Index gebildet wird, $(\downarrow2)(y)=\{\dots,y_{-4},y_{-2},y_{0},y_{2},y_{4},\dots\}$.

Alle diese Operationen zusammengefasst ergibt sich eine gliedweise Berechnungsvorschrift der Analyse-Filterbank

$s_n=\sum_k a_k\cdot x_{2n+k}$ und $d_n=\sum_k b_k\cdot x_{2n+k}$.

Aus der Orthogonalität ergibt sich, dass das Ausgangssignal x zurückgewonnen werden kann, zuerst werden die Tiefpass- und Bandpassanteile s und d in der Abtastrate hochgerechnet, dies wird als Upsampling bezeichnet, mit den Skalierungs- und Waveletmasken gefaltet und dann zusammenaddiert, $2x=a*(\uparrow2)s+b*(\uparrow2)d$ oder koeffizientenweise

$2x_n=\sum_k a_{n-2k}\cdot s_k+\sum_k b_{n-2k}\cdot d_k$.

Der Übergang von x zu (s, d) heißt Analyse, der inverse Synthese. Es ist ersichtlich, dass die Transformierte (s, d) eines endlichen Signals nun etwa genauso viele Samples wie das Signal x selbst hat, also genauso viel Information enthält.

Erweiterungen

Es ist nicht erforderlich, dass die Folgen in der Analyse-Filterbank mit denen in der Synthese-Filterbank wie oben übereinstimmen, nur ist dann nicht garantiert, dass die Kombination beider Filterbänke das Ausgangssignal rekonstruiert. Ist dies doch der Fall, spricht man von vollständiger Rekonstruktion (englisch "perfect reconstruction") oder von Biorthogonalität der Wavelet-Basen.