- Haar-Wavelet
-
Das Haar-Wavelet ist das erste in der Literatur bekannt gewordene Wavelet und wurde 1909 von Alfréd Haar vorgeschlagen.[1] Es ist außerdem das einfachste bekannte Wavelet und kann aus der Kombination zweier Rechteckfunktionen gebildet werden.
Vorteilhaft am Haar-Wavelet ist die einfache Implementierbarkeit der entsprechenden schnellen Wavelet-Transformation (FWT). Der Nachteil des Haar-Wavelets ist, dass es unstetig und daher auch nicht differenzierbar ist.
Inhaltsverzeichnis
Die Funktionen der Haar-Wavelet-Basis
Skalierungsfunktion
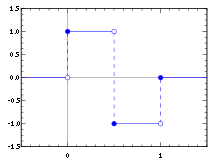
Die Skalierungsfunktion bzw. „Vater-Wavelet“-Funktion der Haar-Wavelet-Basis ist die Indikatorfunktion des Intervalls [0,1).
Sie erfüllt die Funktionalgleichung
 mit
mit  .
.
Waveletfunktion
Die Waveletfunktion ist die „zusammengeschobene“ Differenz zweier aufeinanderfolgender Skalierungsfunktionen:
 ,
,
wobei
 .
.Die Schreibweise mit Vorfaktor sorgt dafür, dass die Matrix
eine orthogonale Matrix ist. Dies ist Teil der Bedingungen, die orthogonale Wavelets erfordern.
Multiskalenanalyse
Diese Funktion erzeugt die Multiskalenanalyse der Stufenfunktionen. In dieser wird jeder Funktion
 mit „endlicher Energie“ auf jeder Skala
mit „endlicher Energie“ auf jeder Skala  die folgende Projektion zugewiesen:
die folgende Projektion zugewiesen: mit
mit  .
.
Die Differenz zwischen zwei Skalen lässt sich dann durch das „Mutter-Wavelet“ bzw. die eigentliche Waveletfunktion ausdrücken:
 .
.
Mit
 und
und  als Funktionen im Hilbertraum
als Funktionen im Hilbertraum  gilt
gilt- alle diese Funktionen haben L2-Norm 1,
- ϕj,k ist senkrecht zu ϕj,l bei k≠l,
- ψi,k ist senkrecht zu ψj,l bei i≠j oder k≠l,
- die ψi,k bilden eine Hilbertbasis von
 .
.
Schnelle Haar-Wavelet-Transformation
Gegeben sei ein diskretes Signal f, welches durch eine endliche oder quadratsummierbare Folge
dargestellt ist. Ihm ist als kontinuierliches Signal die Treppenfunktion
zugeordnet.
Vorwärtstransformation
Aus dem diskreten Signal wird durch paarweises „Senkrechtstellen“ ein vektorwertiges Signal, die sogenannte Polyphasenzerlegung, erzeugt:
 .
.
Dieser wird nun gliedweise mit der Haar-Transformationsmatrix
 multipliziert
multipliziert ,
,
dabei ist
 und
und  .
.Rücktransformation
Wir erhalten ein Mittelwertsignal s und ein Differenzsignal d, aus denen durch einfache Umkehr der vorgenommenen Schritte das Ausgangssignal zurückgewonnen werden kann:
 und
und 
Ist die Schwankung von Glied zu Glied im Ausgangssignal durch ein kleines ε>0 beschränkt, so ist die Schwankung in s durch √2⋅ε beschränkt, also immer noch klein, die Größe der Glieder in d jedoch durch ε/√2. Ein glattes Signal wird also in ein immer noch glattes Signal halber Abtastfrequenz und in ein kleines Differenzsignal zerlegt. Dies ist der Ausgangspunkt für die Wavelet-Kompression.
Rekursive Filterbank
Wir können den Vorgang wiederholen, indem wir s zum Ausgangssignal erklären und mit obigem Vorgehen zerlegen, wir erhalten eine Folge von Zerlegungen
 , sk hat ein 2k-tel der ursprünglichen Abtastfrequenz und eine durch 2k/2⋅ε beschränkte Schwankung, dk hat ebenfalls ein 2k-tel der ursprünglichen Abtastfrequenz und durch 2k/2−1⋅ε beschränkte Glieder.
, sk hat ein 2k-tel der ursprünglichen Abtastfrequenz und eine durch 2k/2⋅ε beschränkte Schwankung, dk hat ebenfalls ein 2k-tel der ursprünglichen Abtastfrequenz und durch 2k/2−1⋅ε beschränkte Glieder.Interpretation
Als diskretes Signal f wird meist eine reelle Folge (fn) über Z mit endlicher Energie betrachtet,
 .
.
Unter diesen gibt es einige sehr einfache Folgen δn, Kronecker- oder Dirac-Delta genannt, eine für jedes n
 Z. Für deren Folgenglieder gilt, dass das jeweils n-te den Wert 1 hat, δnn = 1, und alle anderen den Wert 0, δnk = 0 bei k≠n.
Z. Für deren Folgenglieder gilt, dass das jeweils n-te den Wert 1 hat, δnn = 1, und alle anderen den Wert 0, δnk = 0 bei k≠n.Jetzt können wir jedes Signal trivial als Reihe im Signalraum schreiben
oder als Summe zweier Reihen
 .
.
In vielen praktisch relevanten Signalklassen, z. B. bei überabgetasteten bandbeschränkten kontinuierlichen Signalen, sind Werte benachbarter Folgenglieder auch benachbart, d. h. im allgemeinen liegen f2n und f2n+1 dicht beisammen, relativ zu ihrem Absolutbetrag. Dies wird in der obigen Reihen aber überhaupt nicht berücksichtigt. In Mittelwert und Differenz von f2n und f2n+1 käme deren Ähnlichkeit stärker zum Ausdruck, der Mittelwert ist beiden Werten ähnlich und die Differenz klein. Benutzen wir die Identität
um benachbarte Glieder der ersten Reihe bzw. korrespondierende Glieder in der zweiten Zerlegung zusammenzufassen in (skalierten) Mittelwerten und Differenzen:
Jetzt führen wir neue Bezeichnungen ein:
- die neuen Basisfolgen
-
 und
und 
- mit den neuen transformierten Koeffizienten
-
 und
und  .
.
Wir erhalten somit die Zerlegung der Haar-Wavelet-Transformation
 .
.
und mittels des unendlichen euklidischen Skalarproduktes können wir schreiben
 und
und  .
.
Die letzten drei Identitäten beschreiben eine „Conjugate Quadrature Filterbank (CQF)“, welche so auch für allgemeinere Basisfolgen an und bn definiert werden kann. Die Basisfolgen an entstehen alle durch Verschiebung um das jeweilige 2n aus a0, die bn durch Verschiebung aus b0. Weiteres dazu im Artikel Daubechies-Wavelets.
Nun enthält die Folge s=(sn) eine geglättete Version des Ausgangssignals bei halber Abtastrate, man kann also auch s nach dieser Vorschrift zerlegen und dieses Vorgehen über eine bestimmte Tiefe rekursiv fortsetzen. Aus einem Ausgangssignal s0:=f werden also nacheinander die Tupel
- (s1,d1), (s2,d2,d1), (s3,d3,d2,d1), …
Ist f endlich, also fast überall Null, mit Länge N, dann haben die Folgen in der Zerlegung im Wesentlichen, d. h. bis auf additive Konstanten, die Längen
 ,
,  ,
,  , …
, …
so dass die Gesamtzahl wesentlicher Koeffizienten erhalten bleibt. Die Folgen in der Zerlegung eignen sich meist besser zur Weiterverarbeitung wie Kompression oder Suche nach bestimmtem Merkmalen als das rohe Ausgangssignal.
Modifikationen
Die Polyphasenzerlegung des Ausgangssignals kann auch zu einer anderen Blockgröße s als 2 erfolgen, von der entsprechenden Haar-Matrix ist zu fordern, dass sie eine orthogonale Matrix ist und ihre erste Zeile nur aus Einträgen 1/√s besteht. Diese Anforderung erfüllen die Matrizen der diskreten Kosinustransformation und die der Walsh-Hadamard-Transformation.
Die Haar-Wavelet-Transformation entspricht einer DCT-Transformation zur Blockgröße s=2, welche im Bild=Pixelrechteck nacheinander in horizontaler und vertikaler Richtung angewandt wird.
Literatur
- Alfréd Haar: Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen 69, 331–371, 1910, Online, insbesondere Kapitel 3 (ab S. 361).
Einzelnachweise
- ↑ Alfred Haar: Zur Theorie der orthogonalen Funktionensysteme. In: Mathematische Annalen. 69, Nr. 3, 1910, S. 331–371. doi:10.1007/BF01456326.
Wikimedia Foundation.