Selbstenergie

In der klassischen Physik versteht man unter der Selbstenergie die potentielle Energie einer Ladungsverteilung in ihrem eigenen Feld.

Selbstenergie nennt man auch die störungstheoretischen Korrekturen zum Zweipunktoperator in der Quantenfeldtheorie.

Klassische Verwendung

Das klassische Konzept der Selbstenergie trennt die Ladung und das von ihr erzeugte Feld, um dann herauszufinden, welche Energie nötig wäre, um die Ladung in dieses Feld zu bringen.

Das elektrische Potential ϕ einer Punktladung, die sich an der Position $\vec{r_0}$ befindet, ist am Ort $\vec{r}$ gegeben durch

$\phi = \frac{q}{|\vec{r} - \vec{r_0}|}.$

Eine Punktladung darf nur als der Grenzfall einer endlichen räumlichen Ladungsverteilung mit dem Volumen ΔV angesehen werden. Ist der Abstand zwischen Punktladung und Ort der Potentialmessung $|\vec{r} - \vec{r_0}|$ sehr viel größer als die Ausdehnung der Ladungsverteilung, gilt also

$|\vec{r} - \vec{r_1}| \gg \sqrt[3]{\Delta V},$

so darf man, wie es auch im mechanischen Kraftgesetz mit der idealisierten Punktmasse erfolgt, die Ladungsverteilung in einem Punkt konzentriert als Punktladung ansehen.

Punktladung als Grenzfall einer ausgedehnten Ladungsverteilung

In einer ausgedehnten Ladungsverteilung hat also jedes Volumenelement eine (potentielle) Energie im Feld derselbigen. Solange die Ausdehnungen relativ gesehen groß sind, funktionieren die „gängigen“ Idealisierungen, und $E_\mathrm{pot} = q \cdot \phi$. Lässt man jedoch die Ladungsverteilung in eine Punktladung übergehen, „spürt“ diese ihr eigenes Potential, welches auf eine Singularität zusteuert, da der Abstand $|\vec{r} - \vec{r_0}|$ gegen Null geht, und dadurch gegen unendlich geht.

Eine Punktladung würde in ihrem eigenen Feld ein unendlich hohes Potentialfeld spüren, und somit eine unendlich hohe Energie – eine unendlich hohe Selbstenergie – besitzen. Dies ist jedoch unmöglich.

Daher ist eine Punktladung, wie oben erwähnt, nur solange als ein zutreffendes Modell akzeptabel, wie die beteiligten Abstände groß gegenüber der Ladungsausdehnung sind.

Beispiel: Feldenergie einer homogen geladenen Kugel

Elektrisches Feld:

innen

$r\leq R:\qquad \vec{E}_\text{innen}(\vec{r})=\frac{Q}{4\pi\epsilon_0} \frac{\vec{r}}{R^3}$

außen

$r\geq R:\qquad \vec{E}_\text{aussen}(\vec{r})=\frac{Q}{4\pi\epsilon_0} \frac{\vec{r}}{r^3}$

Feldenergie:

$\begin{align} E_F &= \frac{\epsilon_0}{2}\int dV\vec{E}^2(\vec{r}) = \underbrace{\frac{\epsilon_0}{2}\int^{\infty}_{R} dVE_\text{aussen}^2(r)}_{\text{Arbeit von }\infty\text{ bis R}}+\underbrace{\frac{\epsilon_0}{2}\int^{R}_{0} dVE_\text{innen}^2(r)}_{\text{Arbeit von R bis 0}}\\ &= \frac{\epsilon_0}{2}\frac{Q^2}{(4\pi\epsilon_0)^2}\,4\pi \left( \int^{\infty}_{R} r^2 \frac{1}{r^4}dr+ \int^{R}_{0} r^2 \left(\frac{r}{R^3}\right)^2 dr \right)\\ &= \frac{Q^2}{8\pi\epsilon_0} \left(\frac{1}{R}+\frac{1}{5R}\right)\\ &= \frac{3}{20\pi\epsilon_0 }\frac{Q^2}{R}\end{align}$

Berechnung des Elektronenradius

Mit dem Kugelmodell für Elektronen lässt sich über die Energie auch der „klassische“ Elektronenradius berechnen:

$W = m_e c^2 = \frac{3}{5} \cdot \frac{e^2}{R_e}$.

Quantenfeldtheorie

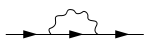
In der Quantenfeldtheorie bezeichnet die Selbstenergie die Beiträgen aller Diagramme mit einer einlaufenden und einer auslaufenden Linie. Als irreduzibler Selbstenergieeinschub (Σ) wird ein Selbstenergieeinschub bezeichnet, der sich nicht durch Auftrennen einer Linie in zwei getrennte Anteile zerlegen lässt. Es werden also beispielsweise in diesem Fall nicht die Diagramme erfasst, in denen mehrere Schleifen getrennt hintereinander folgen. Die Selbstenergie wird dann als Summe der Beiträge aller irreduziblen Selbstenergieeinschübe definiert:

Ein Selbstenergiediagramm heißt Skelett, falls es ausschließlich aus Propagatoren aufgebaut wird, die keine Selbstenergieeinschübe, also Schleifen, beinhalten. Ein angezogenes Skelett ist ein Skelett aus der Entwicklung der Selbstenergie, bei dem jeder freie Propagator durch einen Propagator ersetzt wurde, der um die Selbstenergie korrigiert wurde. Damit ist die Selbstenergie die Summe der Beiträge aller angezogenen Skelette. Die Darstellung Selbstenergie als Summe der Beiträge aller angezogenen Skelette und die Dyson-Gleichung bilden ein Gleichungssystem, das gleichzeitig (selbstkonsistent) zu lösen ist. Dies kann iterativ geschehen, bis bei Selbstkonsistenz abgebrochen werden kann. Dies führt auf die selbstkonsistente Renormierung.

Der einfachste Fall der Dyson-Gleichung (Zweipunktfunktion) betrachtet gerade die Selbstenergie.