- Potentielle Energie
-
 Potentielle Energie im Wasserkraftwerk nutzbar gemacht
Potentielle Energie im Wasserkraftwerk nutzbar gemacht
Die potentielle Energie (auch Höhen- oder Lageenergie) stellt in der Physik eine Form der Energie dar. Diese Energie nimmt zu oder ab, wenn sich ein Körper entgegen oder gleich der Richtung der Gewichtskraft (Schwerkraft) bewegt. Verallgemeinert tritt eine solcher Energieumsatz nicht nur im Erdschwerefeld auf, sondern bei allen konservativen Kraftfeldern, etwa dem elektrischen Feld, weshalb der Begriff potentielle Energie auch dort Anwendung findet. Der mathematische Ansatz ist ebenfalls identisch.
Als Formelzeichen für die potentielle Energie wird üblicherweise Epot, U oder V verwendet.
Inhaltsverzeichnis
Heranführung
Ein Radfahrer erreicht auf ebener Strecke ohne viel Mühe 20 km/h, da er nur gegen den Luftwiderstand und die Rollreibung antreten muss. Kommt er nun an einen ansteigenden Streckenabschnitt muss er sich bei gleicher Geschwindigkeit stärker anstrengen als zuvor. Nach erreichen der Kuppe geht es bergab und der Radfahrer rollt ohne Tretbewegungen weiter, muss sogar bremsen, damit er nicht zu schnell wird.
Auf den Fahrer samt Rad wirken zwei Kräfte die Reibungskraft und die Gewichtskraft. Im ersten Streckenabschnitt zeigt die Gewichtskraft senkrecht zur Straße und weist somit nach Anwendung der Kräftezerlegung keine Kraftkomponente in Bewegungsrichtung auf. Kommt nun ein Anstieg ergibt die Zerlegung der Gewichtskraft eine Kraftkomponente entgegen der Bewegungsrichtung. Nach überschreiten der Kuppe hat die Schwerkraft eine Komponente in Bewegungsrichtung und entgegen der Reibungskraft.
Für eine Bewegung entgegen der Gewichtskraft muss am Körper Arbeit aufgewendet werden, die nun als potentielle Energie in ihm gespeichert ist. Bei einer Bewegung die eine Komponente in Richtung der Gewichtskraft enthält leistet der Körper Arbeit, überwindet etwa Reibungsverluste und seine potentielle Energie nimmt ab. Die Wegkomponente in Richtung Gewichtskraft heißt Höhe und zusammen mit der Kraft ergibt sich:
- m – Masse
- g – Erdbeschleunigung
- h – Höhe über dem Boden
- Bedingung: Höhe deutliche geringer als der Erdradius h ≪ RE)
Formale Definition
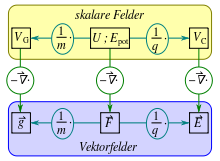 Potential- und Gradientenfeldern in der Physik
Potential- und Gradientenfeldern in der Physik
skalare Felder (Potentialfelder):
VG – Gravitationspotential
Epot – potentielle Energie
VC – Coulomb-Potential
Vektorfelder (Gradientenfelder):
g – Gravitationsbeschleunigung
F – Kraft
E – elektrische FeldstärkeDa ein konservatives Kraftfeld die Kraft
 auf einen Probekörper an einem beliebigen Ort definiert und mathematisch ein Gradientenfeld ist, existiert auch ein skalares Feld
auf einen Probekörper an einem beliebigen Ort definiert und mathematisch ein Gradientenfeld ist, existiert auch ein skalares Feld  der potentiellen Energie für den jeweiligen Ort. Aus der Umkehrung des Arbeitsintegrals folgt, das der Energieanstieg entlang einem Weg eine Kraftkomponente entgegen dem Weg voraussetzt. Durch Zerlegung des Feldes in kartesische Komponenten ergeben sich in Abhängigkeit vom Ort folgende partielle Ableitungen:
der potentiellen Energie für den jeweiligen Ort. Aus der Umkehrung des Arbeitsintegrals folgt, das der Energieanstieg entlang einem Weg eine Kraftkomponente entgegen dem Weg voraussetzt. Durch Zerlegung des Feldes in kartesische Komponenten ergeben sich in Abhängigkeit vom Ort folgende partielle Ableitungen:Allgemein lässt sich dies durch den Nabla-Operator
 ausdrücken.
ausdrücken.Die Umkehrung der Ableitung führt zum Integral und ermittelt die Änderung der potentiellen Energie im Kraftfeld als Arbeitsintegrals mit negativem Vorzeichen. Hieran zeigt sich auch nachvollziehbar die Übertragbarkeit auf verschiedene Kraftfelder.
Um die potentielle Energie eines Körpers zu vergrößern, muss Feldarbeit gegen die Kräfte eines konservativen Kraftfeldes verrichtet werden. So besitzt jeder massebehaftete Körper in einem Gravitationsfeld potentielle Energie. Diese kann jedoch nur erhöht oder vermindert werden, wenn der Körper gegen oder in Richtung der Gravitationskraft verschoben wird. Bei einer Verschiebung senkrecht zu den Feldlinien behält der Körper seine potentielle Energie bei. Ein solcher Bereich nennt sich Äquipotentialfläche oder -linie und entspricht einer Höhenlinie auf der Landkarte. Die Feldlinie dagegen beschreibt die Richtung der Steigung.
Sofern keine Reibungsverluste oder sonstige Wechselwirkungen mit der Umgebung auftreten gilt für eine Verschiebung in konservativen Kraftfeldern das Prinzip der Wegunabhängigkeit. Das bedeutet unabhängig vom eingeschlagenen Weg muss gleich viel Feldarbeit verrichtet werden damit ein Körper vom Ausgangspunkt zum Zielpunkt gelangt. Hierin spielt sich der Energieerhaltungssatz wieder, da die Arbeit der Energieänderung entspricht.
Die Wahl des Bezugsniveau kann beliebig erfolgen, jedoch reduzieren pragmatischen Gründe die Auswahl. Im Zweifelsfall immer als Nullniveau geeignet ist der Ausgangspunkt des untersuchten Körpers. Beim Gravitationsfeld bildet häufig die Erdoberfläche den Bezugspunkt oder allgemein der niedrigste Punkt der Umgebung. Darüber hinaus kann der Bezugspunkt an einen unendlich weit entfernten Ort verlegt werden (
 ). Die Umkehrung davon bildet die maximale potentielle Energie, bei der ein Körper von seinem Ausgangspunkt aus dem Kraftfeld heraus bewegt wird, wobei ein zentrales Kraftfeld angenommen sei.
). Die Umkehrung davon bildet die maximale potentielle Energie, bei der ein Körper von seinem Ausgangspunkt aus dem Kraftfeld heraus bewegt wird, wobei ein zentrales Kraftfeld angenommen sei.Bei elektrischer Ladungen entgegengesetzten Vorzeichens führt dies zur minimalen potentiellen Energie.
Potentielle Energie und der Energieerhaltungssatz
In einem abgeschlossenen System ohne Energieaustausch mit der Umgebung und unter Vernachlässigung jedweder Reibung gilt zu jedem Zeitpunkt der Energieerhaltungssatz der klassischen Mechanik:
- E = T + U = const.
- U - potentielle Energie
- T - kinetische Energie
- E - mechanische Energie
In Worten: Die Summe aus potentieller und kinetischer Energie, einschließlich der Rotationsenergie, ist konstant und entspricht der Gesamtenergie des mechanischen Systems.
In einer höheren Formulierung der Mechanik, dem Hamilton-Formalismus, schreibt man auch
wobei H die Hamiltonfunktion und L die Lagrangefunktion sind.
Potentielle Energie im Gravitationsfeld
Die Kraft auf eine Masse in einem gegebenen Gravitationsfeld errechnet sich aus:
Durch Einsetzen in das Arbeitsintegral zeigt sich nun die Beziehung zwischen der potentiellen Energie einer Masse und dem Gravitationspotential das ebenfalls ein Skalarfeld darstellt. Beide Felder unterscheidet nur der Proportionalitätsfaktor Masse.
Um den Massenpunkt von einer Planetenoberfläche R aus dem Gravitationsfeld heraus, also in die Unendlichkeit, zu befördern, muss die maximale potentielle Energie des Gravitationsfeldes des Planeten gerade erreicht oder übertroffen werden. Für diese gilt:
In der Kosmologie ist die sogenannte Gravitationsenergie die größte bekannte Energiequelle und führt über die kinetische Energie zu den kosmischen Geschwindigkeiten.
Potentielle Energie im elektrischen Feld
Die Kraft auf eine Ladung in einem gegebenen elektrischen Feld errechnet sich aus:
Durch einsetzen in das Arbeitsintegral zeigt sich nun die Beziehung zwischen der potentiellen Energie einer Ladung und dem Coulombpotential das ebenfalls ein Skalarfeld darstellt. Beide Felder unterscheidet nur der Proportionalitätsfaktor Masse.
Das Coulombpotential wird oft als φ statt VC geschrieben.
Potentielle Energie einer gespannten Feder
Aus der Federkraft
- F(x) = − kx,
ergibt sich für die potentielle Energie
 .
.
Hierbei ist k die Federkonstante und x die Auslenkung der Feder aus der Ruhelage.
Weblinks
 Commons: Potential energy – Sammlung von Bildern, Videos und Audiodateien
Commons: Potential energy – Sammlung von Bildern, Videos und Audiodateien
Wikimedia Foundation.











![U_\mathrm{max}=\int_{R}^{\infty} \frac{GMm}{R^2}\, \mathrm{d}R=GMm\int_{R}^{\infty} \frac{1}{R^2}\, \mathrm{d}R=GMm\left[-\frac{1}{R}\right]^\infty_R=\frac{GMm}{R}=m \, g \, R](5/53564ce6e05fb43d163071e92e2cf5f7.png)

