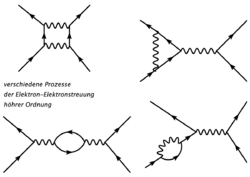
Feynman-Graph

Feynman-Diagramm eines Beitrags zur Elektron-Elektron-Streuung durch Austausch eines virtuellen Photons (Zeitachse von unten nach oben).

Ein-Loop-Beiträge zur Elektron-Elektron-Streuung

Feynman-Diagramme (nach Richard Feynman) stellen in der Teilchenphysik und der Festkörperphysik die quantenfeldtheoretischen Beiträge zu Streuvorgängen bildlich dar und veranschaulichen und erleichtern so ihre Berechnung.

Feynman-Diagramme haben äußere Linien, die in Wechselwirkungspunkte ein- oder auslaufen, und innere Linien, die Paare von Wechselwirkungspunkten verbinden. Den äußeren Linien entsprechen ein- und auslaufende Teilchen. Die inneren Linien nennt man Propagatoren und deutet sie als virtuelle Teilchen. Die Wechselwirkungspunkte, an denen Linien zusammentreffen, heißen auch Vertizes. An ihnen können Teilchen erzeugt, vernichtet oder gestreut werden.

Geladene Teilchen kennzeichnet man durch Pfeile in Zeitrichtung, Antiteilchen durch Pfeile in Gegenrichtung. Die Pfeile geben also den Ladungsfluss an. Ungeladene Teilchen, die ihre eigenen Antiteilchen sind, wie zum Beispiel Photonen, haben keine Pfeile.

Es sind beliebig viele Diagramme denkbar. Die Diagramme lassen sich nach der Zahl der inneren Schleifen ordnen (Loop-Ordnung). Bei genügend schwacher Kopplung werden die Beiträge höherer Ordnung, so die Arbeitshypothese der Störungstheorie, numerisch vernachlässigbar.

Diagramme ohne Schleifen haben die Struktur eines Baumes (Stamm, von dem Äste verzweigen) und heißen Baumdiagramme.

Beispiel

Zur Berechnung beispielsweise der Streuung zweier Elektronen betrachtet man Feynman-Diagramme mit zwei einlaufenden und zwei auslaufenden Elektronen. Jedem dieser Diagramme entspricht ein Beitrag zur Streuung, der gesamte Streuvorgang wird durch die Summe aller Diagramme dargestellt. Das obere Bild zeigt die Elektron-Elektron-Streuung (Møller-Streuung) in niedrigster Ordnung („Tree-Level“). Die vier äußeren Linien stehen für die ein- und auslaufenden Elektronen, die innere Wellenlinie für das virtuelle Photon, das die elektromagnetische Wechselwirkung bewirkt. Die Berechnung dieser Streuung und allgemeiner die Feynman-Regeln für die mathematischen Ausdrücke, die den Linien und Vertizes entsprechen, finden sich in vielen Lehrbüchern der Teilchenphysik.

Typen von Feynman-Diagrammen

• Zusammenhängende Diagramme:

  Ist jeder Vertex über innere Linien und andere Vertizes mit jedem anderen Vertex verbunden, so bezeichnet man das Diagramm als zusammenhängend, anderenfalls als unzusammenhängend. Bei jedem zusammenhängenden Teil des Diagramms ist die Summe der Energien, Impulse und Ladungen der einlaufenden Teilchen gleich der Summe der Energien, Impulse und Ladungen der auslaufenden Teilchen.

• Ein-Teilchen-irreduzible Diagramme:

  Kann ein zusammenhängendes Diagramm nicht durch Zerschneiden einer inneren Linie in zwei unzusammenhängende Diagramme geteilt werden, so heißt es Ein-Teilchen-irreduzibel. Bei solchen Diagrammen treten Integrationen auf, die man nicht systematisch als Produkt einfacherer Integrale vereinfachen kann.

• Amputierte Diagramme:

  Lässt man bei einem Diagramm die äußeren Linien weg, so bezeichnet man es als amputiert.

• Selbstenergie-Diagramme:

  Ein Diagramm mit einem Loop und mit äußeren Linien an nur zwei Vertizes heißt (nach Amputation) Selbstenergiediagramm. Sein Wert hängt nur von der Energie und dem Impuls ab, der durch äußere Linien an dem einem Vertex hinein- und an dem anderen hinaus fließt.

• Skelett-Diagramme:

  Ein Diagramm ohne ein Selbstenergie-Unterdiagramm bezeichnet man als Skelett-Diagramm.

Siehe auch

• Møller-Streuung
• Compton-Streuung
• Paarvernichtung
• Paarbildung
• Selbstenergie
• Vakuumpolarisation
• Pinguin-Diagramm

Literatur

• Otto Nachtmann, Phänomene und Konzepte der Elementarteilchenphysik, Vieweg, Braunschweig, 1986 ISBN 3-528-08926-1

Weblinks

• Feynman-Diagramme (engl.)
• Using Feynman diagrams to illustrate particle interactions in the Standard Model (engl.)