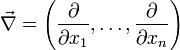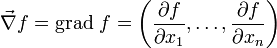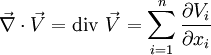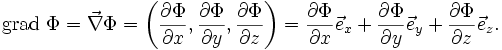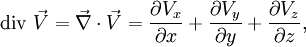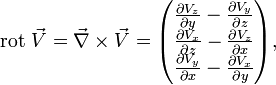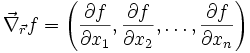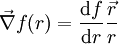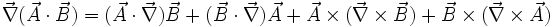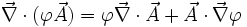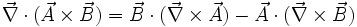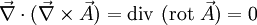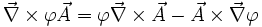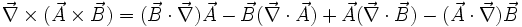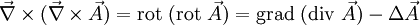Nabla-Kalkül

Der Nabla-Operator ist ein Operations-Symbol, das in der Vektoranalysis benutzt wird, um die drei Differentialoperatoren Gradient, Divergenz und Rotation zu bezeichnen. Er wird durch das Nabla-Symbol $\nabla$ bezeichnet oder durch $\vec{\nabla}$ (im englischen Sprachraum 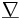$\underline \nabla$), um seine Ähnlichkeit zu einem Vektor zu betonen. Sein Name stammt von der Bezeichnung eines hebräischen Saiteninstruments, das in etwa die Form dieses Zeichens hatte.

Formal ist der Nabla-Operator ein (Spalten-)Vektor, dessen Komponenten die partiellen Ableitungsoperatoren 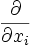$\frac\partial{\partial x_i}$ sind:

$\vec\nabla = \left (\frac\partial{\partial x_1},\ldots, \frac\partial{\partial x_n}\right)$

bzw. im 3-dimensionalen kartesischen Koordinatensystem:

$\vec\nabla = \left(\frac\partial {\partial x}, \frac\partial {\partial y}, \frac\partial {\partial z}\right) = \vec e_1 \frac\partial {\partial x} + \vec e_2 \frac\partial {\partial y} + \vec e_3 \frac\partial {\partial z}$

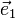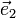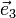Dabei sind hier $\vec e_1$, $\vec e_2$ und $\vec e_3$ die 3 Einheitsvektoren des Koordinatensystems.

Gerechnet wird mit dem Nabla-Operator wie mit einem Vektor, wobei das „Produkt“ von 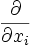$\frac\partial{\partial x_i}$ mit einer rechts davon stehenden Funktion f als partielle Ableitung 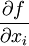$\frac{\partial f}{\partial x_i}$ interpretiert wird.

Allgemeiner Fall

Im n-dimensionalen Raum 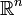$\mathbb R^n$ liefert das (formale) Produkt von $\vec\nabla$ mit einer Funktion (Skalarfeld) deren Gradienten:

$\vec\nabla f = \operatorname{grad\ } f = \left (\frac{\partial f}{\partial x_1},\ldots, \frac{\partial f}{\partial x_n}\right)$

Das (formale) Skalarprodukt mit einem Vektorfeld 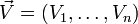$\vec V = (V_1, \dots, V_n)$ ergibt dessen Divergenz:

$\vec\nabla \cdot \vec V = \operatorname{div\ } \vec{V} = \sum_{i=1}^n \frac{\partial V_i}{\partial x_i}$

Spezialfall im Dreidimensionalen

Im dreidimensionalen Raum mit den kartesischen Koordinaten x, y, z stellen sich die obigen Formeln wie folgt dar:

• Angewandt auf ein Skalarfeld 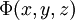$\begin{matrix} \Phi(x,y,z) \end{matrix}$ erhält man den Gradienten des Skalarfeldes

$\operatorname{grad\ }\Phi = \vec\nabla \Phi = \left(\frac{\partial\Phi}{\partial x}, \frac{\partial\Phi}{\partial y}, \frac{\partial\Phi}{\partial z}\right) = \frac{\partial\Phi}{\partial x} \vec e_x + \frac{\partial\Phi}{\partial y} \vec e_y + \frac{\partial\Phi}{\partial z} \vec e_z.$

Das Ergebnis ist ein Vektorfeld, 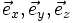$\vec e_x, \vec e_y, \vec e_z$ sind die kartesischen Einheitsvektoren des $\mathbb R^3$.

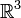• Angewandt auf ein Vektorfeld 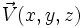$\begin{matrix} \vec{V}(x, y, z) \end{matrix}$ ergibt sich die Divergenz des Vektorfeldes als formales Skalarprodukt mit dem Vektorfeld zu

$\operatorname{div\ }\vec{V} = \vec{\nabla} \cdot \vec{V} = \frac{\partial V_x}{\partial x} + \frac{\partial V_y}{\partial y} + \frac{\partial V_z}{\partial z},$

also ein Skalarfeld.

• Eine Besonderheit des dreidimensionalen Raums ist die Rotation eines Vektorfelds. Sie ergibt sich durch (rechtsseitige) Verknüpfung über das formale Kreuzprodukt als

$\operatorname{rot\ }\vec{V} = \vec{\nabla} \times \vec{V} = \begin{pmatrix} \frac{\partial V_z}{\partial y} - \frac{\partial V_y}{\partial z} \\ \frac{\partial V_x}{\partial z} - \frac{\partial V_z}{\partial x} \\ \frac{\partial V_y}{\partial x} - \frac{\partial V_x}{\partial y} \\ \end{pmatrix},$

also wieder ein Vektorfeld.

Notation mit Subskript

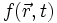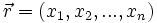Wirkt der Nablaoperator nur auf bestimmte Komponenten einer Funktion mit einem mehrdimensionalen Argument, so wird dies durch ein Subskript angedeutet. Für eine Funktion $f(\vec{r},t)$ mit $\vec{r}=(x_1, x_2, ..., x_n)$ beispielsweise ist

$\vec\nabla_{\vec{r}} f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n}\right)$

im Gegensatz zu

$\vec\nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n}, \frac{\partial{f}}{\partial t}\right)$.

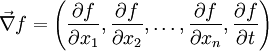Rechenregeln

Rechenregeln für den Nabla-Operator lassen sich formal aus den Rechenregeln für Skalar- und Kreuzprodukt zusammen mit den Ableitungsregeln herleiten. Dabei muss man die Produktregel anwenden, wenn der Nabla-Operator links von einem Produkt steht.

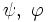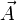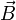Sind $\psi,~\varphi$ und f Skalarfelder (Funktionen) und $\vec A$ und $\vec B$ Vektorfelder, so gilt:

$\vec\nabla f(r)=\frac{\mathrm d f}{\mathrm d r}\frac{\vec r}{r}$

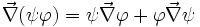$\vec\nabla(\psi\varphi)=\psi\vec\nabla\varphi+\varphi\vec\nabla\psi$ (Produktregel für Gradient)

$\vec\nabla(\vec A\cdot\vec B)=(\vec A\cdot\vec\nabla)\vec B+(\vec B\cdot\vec\nabla)\vec A+\vec A\times(\vec\nabla\times\vec B)+\vec B\times(\vec\nabla\times\vec A)$

$\vec\nabla\cdot(\varphi\vec A)=\varphi\vec\nabla\cdot\vec A+\vec A\cdot\vec\nabla\varphi$

$\vec\nabla\cdot(\vec A\times\vec B)=\vec B\cdot(\vec\nabla\times\vec A)-\vec A\cdot(\vec\nabla\times\vec B)$

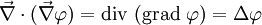$\vec\nabla\cdot(\vec\nabla\varphi)=\operatorname{div\ }(\operatorname{grad\ }\varphi)=\Delta\varphi$ (siehe auch Laplace-Operator)

$\vec\nabla\cdot(\vec\nabla\times\vec A)=\operatorname{div\ }(\operatorname{rot\ }\vec A)=0$

$\vec\nabla\times(\vec\nabla\varphi)=\operatorname{rot\ }(\operatorname{grad\ }\varphi)=0$

$\vec\nabla\times\varphi\vec A=\varphi\vec\nabla\times \vec A-\vec A\times\vec\nabla\varphi$

$\vec\nabla\times (\vec A\times\vec B)=(\vec B\cdot\vec\nabla)\vec A-\vec B(\vec\nabla\cdot\vec A)+\vec A(\vec\nabla\cdot\vec B)-(\vec A\cdot\vec\nabla)\vec B$

$\vec\nabla\times (\vec\nabla\times \vec A)=\operatorname{rot\ }(\operatorname{rot\ }\vec A)=\operatorname{grad\ }(\operatorname{div\ }\vec A) -\Delta\vec A$

Weitere Rechenregeln siehe unter Gradienten, Divergenz und Rotation.

Siehe auch: Formelsammlung Nabla-Operator

Literatur

• Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 5. Auflage. Harri Deutsch, 2001, ISBN 3817120052 (Enthält alle hier genannten Eigenschaften, jedoch ohne Beweis.). 
• Jänich: Vektoranalysis. Springer, 1992, ISBN 3540555307 (Enthält nur die grundlegende Definition.). 
• Großmann: Mathematischer Einführungskurs für die Physik. Teubner, Stuttgart 1991 (siehe insbesondere Abschnitt 3.6).