Richtungsableitung

In der Mathematik ist die Richtungsableitung einer von mehreren Variablen abhängigen Funktion die momentane Änderungsrate dieser Funktion in einer durch einen Vektor vorgegebenen Richtung.

Eine Verallgemeinerung der Richtungsableitung auf unendlichdimensionale Räume ist das Gâteaux-Differential.

Definitionen

Seien ${U}\subseteq \mathbb{R}^n$ eine offene Menge, $\vec{x}\in {U}$ und $\vec{v} = (v_1, \ldots, v_n)\in \mathbb{R}^n$ ein Einheitsvektor (das heißt $|\vec{v}| = 1$).

Die (beidseitige) Richtungsableitung einer Funktion $f\colon {U} \rightarrow \mathbb{R}$ am Punkt $\vec x$ entlang (oder in Richtung von) $\vec{v}$ ist definiert durch den Limes

$D_{\vec{v}}{f(\vec{x})} = \lim_{h \rightarrow 0}{\frac{f(\vec{x} + h\vec{v}) - f(\vec{x})}{h}},$

falls der Grenzwert existiert.

Eine alternative Formulierung ist folgende:

Durch $t \mapsto f(\vec x + t \vec v)$ ist eine Funktion $g_{\vec v} \colon \R \to \R$ definiert mit $g_{\vec v}(0) = f(\vec x)$. Ihre Ableitung an der Stelle t = 0 ist gerade die Richtungsableitung von f im Punkt $\vec x$ in Richtung $\vec v$.

$D_{\vec v} f(\vec x) = g_{\vec v}'(0) = \frac{d}{dt}f(\vec x + t \vec v)\Big|_{t=0}$

Verzichtet man auf die Einschränkung $|\vec{v}| = 1$, so gibt es zwei Möglichkeiten, den Begriff „Ableitung entlang oder in Richtung von $\vec v$“ zu interpretieren:

1. Übernimmt man die obenstehenden Definitionen, so ist $D_{\vec v} f(\vec x)$ proportional zur Länge von $\vec v$.
2. Soll der Wert der Richtungsableitung nur von der Richtung von $\vec v$ abhängen, aber nicht von der Länge, so muss die Definition modifiziert werden, zum Beispiel zu

   $\tilde D_{\vec{v}}{f(\vec{x})} = \lim_{h \rightarrow 0}{\frac{f(\vec{x} + h\vec{v}) - f(\vec{x})}{h\left|\vec v\right|}}$

Im Folgenden wird der erste Ansatz zu Grunde gelegt.

Schreibweisen

Statt $D_{\vec v} f (\vec x)$ sind auch die Schreibweisen

$\nabla_{\vec{v}}{f}(\vec{x})$,   $\partial_{\vec v} f(\vec x)$,   $\frac{\partial{f(\vec{x})}}{\partial{\vec v}}$   und $f'_\vec{v}(\vec{x})$

üblich, um unter anderem Verwechslungen mit den kovarianten Ableitungen der Differentialgeometrie zu vermeiden.

Ist f total differenzierbar, so kann die Richtungsableitung mit Hilfe der totalen Ableitung dargestellt werden (siehe den Abschnitt Eigenschaften). Schreibweisen dafür sind

$Df(\vec x) \vec v$,   $Df_{\vec x} \, \vec v$,   $\operatorname{grad}\ f(\vec x) \cdot \vec v$,   $\nabla f(\vec x) \cdot \vec v$   und $(\vec v \cdot \nabla) f (\vec x)$.

Bei allen Formen sind auch Schreibweisen ohne Vektorpfeile üblich und solche, bei denen Punkte und Vektoren durch Fettdruck von Skalaren unterschieden werden.

Einseitige Richtungsableitung

Die einseitige Richtungsableitung von $f\colon {U} \rightarrow \mathbb{R}$ in Richtung $\vec{v}\in\mathbb{R}^{n}$ ist definiert durch

$D^{+}_{\vec{v}}{f(\vec{x})} = \lim_{h \rightarrow 0, h>0}{\frac{f(\vec{x} + h\vec{v}) - f(\vec{x})}{h}}.$

Die beidseitige Richtungsableitung in Richtung $\vec{v}$ existiert genau dann, wenn

$D^{+}_{-\vec{v}}{f(\vec{x})} = -D^{+}_{\vec{v}}{f(\vec{x})}.$

In diesem Fall gilt

$D_{\vec{v}}{f(\vec{x})} = D^{+}_{\vec{v}}{f(\vec{x})} = -D^{+}_{-\vec{v}}{f(\vec{x})}.$

Eigenschaften

• Wählt man als Richtungsvektor $\vec v$ die Koordinateneinheitsvektoren $\vec e_1, \dots, \vec e_n$, so erhält man die partiellen Ableitungen:

  $D_{\vec e_i} f = \frac{\partial f}{\partial x_i}$

• Die einseitige Richtungsableitung ist als Funktion von $\vec{v}$ positiv homogen, das heißt für alle positiven α > 0 gilt:

  $D^{+}_{\alpha\vec{v}}{f(\vec{x})}=\alpha D^{+}_{\vec{v}}{f(\vec{x})}.$

• Falls f in $\vec{x}$ total differenzierbar ist, so ist die Richtungsableitung als Funktion von $\vec{v}$ sogar linear und kann durch den Gradienten $\nabla f$ von f ausgedrückt werden:

  $D_{\vec{v}}{f}(\vec x) = \nabla f(\vec x) \cdot \vec{v} = \frac{\partial f}{\partial x_1}(\vec x) \,v_1 + \dots +\frac{\partial f}{\partial x_n}(\vec x)\, v_n$

Beispiel

Absolutbetrag=seine Richtungsableitung in 0

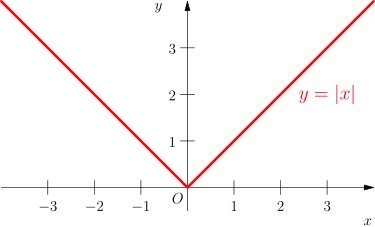
Im eindimensionalen Fall gibt es nur zwei mögliche Richtungen, nämlich nach links bzw. nach rechts. Die Richtungsableitungen entsprechen also den üblichen einseitigen Ableitungen. Die Ableitungen in beide Richtungen dürfen verschiedene Werte annehmen, das bedeutet anschaulich, dass die Funktion einen Knick haben kann. Ein einfaches Beispiel hierfür ist die Betragsfunktion. Sie ist in 0 zwar nicht differenzierbar, aber die einseitige Richtungsableitung existiert:

$D^{+}_{h}{f(0)}=h$ für $h\geq 0$ und

$D^{+}_{h}{f(0)}=-h$ für $h \leq 0$

Der Absolutbetrag ist also gleich seiner einseitigen Richtungsableitung in 0 als Funktion von h.

Literatur

• Otto Forster: Analysis 2. Differentialrechnung im Rⁿ. Gewöhnliche Differentialgleichungen. Vieweg-Verlag, 7. Aufl. 2006, ISBN 3-528-47231-6
• Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8