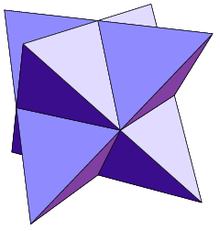
- Sterntetraeder
-
Das Sterntetraeder, auch bekannt als Sternkörper zum Oktaeder und als Keplerstern, ist ein achtstrahliger Stern und gehört zu den nicht-konvexen Deltaedern. Es handelt sich um einen vielflächigen Körper, der durch Verschmelzung zweier punktsymmetrischer Tetraeder entsteht. Entdeckt und benannt durch Johannes Kepler (daher der Name „Keplerstern“) im Jahr 1609, ist dies sowohl das einfachste reguläre zusammengesetzte Polyeder als auch das einfachste nicht-konvexe gleichmäßige Polyeder.
Die äußeren Eckpunkte des Körpers beschreiben einen Würfel, während die Schnittmenge der beiden Tetraeder ein Oktaeder darstellt, dessen Kanten wiederum die Innenkanten des Sterntetraeders darstellen.
Der Grafiker M. C. Escher hat das Sterntetreaeder als Motiv für das Bild Doppelplanetoid verwendet: Das eine Tetraeder hat die Form einer von Menschen bewohnten Burg, während das andere eine mit dem ersten durchdrungene, von Dinosauriern bewohnte Welt darstellt.[1]
Das Sterntetraeder ist die erste Stufe der konvexen Form des Sierpinski-Oktaeders.[2] Aus den acht kleinen Tetraedern können wieder Sterntetraeder gemacht werden, und dieser Vorgang kann wiederholt werden, so dass schließlich ein Fraktal entsteht, welches sich der Form eines Hexaeders annähert.[3][4]
Einzelnachweise
Wikimedia Foundation.