Steuerbetragsfunktion

Unter einer Steuerbetragsfunktion versteht man die vollständige, funktionale Zuordnung eines bestimmten Steuerbetrags S zur zugrunde gelegten Bemessungsgrundlage B. So legt beispielsweise die Steuerbetragsfunktion bei der Einkommensteuer fest, welcher Steuerbetrag (in Euro) von einem gegebenen zu versteuernden Einkommen (Bemessungsgrundlage) zu bezahlen ist.

Steuerbetragsfunktionen (Prinzip):
grün = proportional
rot = progressiv (überproportional)
blau = degressiv (unterproportional)
gelb = degressiv (Steuerbetrag konstant)

Meist wird dazu eine mathematische Funktion definiert

$S\!\, = S(B)$

Dabei gibt es mehrere Möglichkeiten, den Funktionsverlauf festzulegen, wobei im Steuerrecht der Begriff Steuertarif üblich ist:

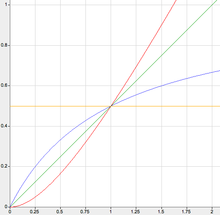
• Proportionaler Tarif mit konstantem Steuersatz (Flat Tax)
• Progressiver Tarif mit steigendem Steuersatz
• Degressiver Tarif mit sinkendem Steuersatz
• Pauschaltarif mit konstantem Steuerbetrag (Kopfsteuer)

jeweils in Abhängigkeit von der Bemessungsgrundlage. Das nebenstehende Bild (Prinzipdarstelllung) zeigt dazu auf der senkrechten Achse den Steuerbetrag und auf der waagrechten Achse die Bemessungsgrundlage.

Diese Funktion muss jedoch nicht an jeder Stelle stetig und differenzierbar sein. Mit anderen Worten: Tarife müssen nicht für jeden Bereich der Steuerbemessungsgrundlage die gleiche Eigenschaft in gleichem Ausmaß aufweisen. So kann beispielsweise die Einkommensteuer erst ab einem bestimmten Mindesteinkommen einsetzen (Grundfreibetrag) oder ab einem bestimmten Einkommen sprunghaft ansteigen. Finanzwissenschaftler unterscheiden oft die folgenden Spezifikationen:

• Stufengrenzsatztarif,
• Stufenbetragstarif und
• Stufendurchschnittstarif.

Die Steuerbetragsfunktion kann mittels zweier Größen analysiert werden:

dem Durchschnittssteuersatz s und dem Grenzsteuersatz s_g, wobei

$s = \bar s = \frac {S(B)} {B}$

$s_{g} = S' = \frac {\mbox{d} S(B)} {\mbox{d} B}$

Der Durchschnittssteuersatz (in Prozent) gibt an, wie hoch der Anteil des Steuerbetrages im Verhältnis zur gesamten Bemessungsgrundlage ist, während der Grenzsteuersatz (ebenfalls in Prozent) anzeigt, wie viel Steuer auf eine zusätzliche Einheit der zugrunde gelegten Bemessungsgrundlage zu entrichten ist (beispielsweise: „wie viel Lohnsteuer muss ich zusätzlich zahlen, wenn ich einen Euro mehr verdiene?“).