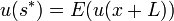Sä

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Das Sicherheitsäquivalent ist ein Begriff aus der Entscheidungstheorie. Es bezeichnet denjenigen sicheren Wert bzw. Geldbetrag, bei dem ein Entscheider, der eine Lotterie L besitzt, indifferent ist, diese zu behalten oder abzugeben.

Formale Beschreibung

Sei L eine Lotterie mit der Konsequenzenmenge x_i und den dazugehörigen Wahrscheinlichkeiten p_i. Des Weiteren seien u eine stetige Nutzenfunktion, mit der Umkehrfunktion u ^{− 1}, und x ein sicheres Ausgangsvermögen eines Entscheiders. Die Gleichung

$\!\, u(s^*) = E(u(x+L))$

beschreibt, dass der Nutzen des Sicherheitsäquivalents gleich dem Erwartungswert des Nutzens der Lotterie L ist. Somit ist der Entscheider indifferent zwischen der unsicheren Lotterie und dem Sicherheitsäquivalent. Umgeformt ergibt sich daher für s* folgende Gleichung

$\!\, s^* = u^{-1}(E(u(x+L)))$.

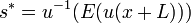Strategien

Für risikoaverse Entscheider ist das Sicherheitsäquivalent strikt kleiner als der Erwartungswert der Lotterie. Ein risikoaverser Entscheider ist somit bereit, eine Lotterie L, die er besitzt, zu einem kleineren Betrag als dem Erwartungswert abzugeben. Der Unterschiedsbetrag zwischen Sicherheitsäquivalent und dem Erwartungswert der Lotterie wird als Risikoprämie bezeichnet.

Für risikofreudige Entscheider ist das Sicherheitsäquivalent strikt größer als der Erwartungswert der Lotterie während bei risikoneutralen Entscheidern sich Sicherheitsäquivalent und Erwartungswert der Lotterie entsprechen.

Eine risikoaverse Strategie ist gegenüber der risikoneutralen Strategie insbesondere bei großen potenziellen Gewinnen sehr praxisrelevant. Der Grund dafür liegt in dem abnehmenden Grenznutzen, z. B. bei einem Gewinn in Geld. Anschaulich betrachtet wäre es für einen mittellosen Entscheider eher ungeschickt, etwa ein Sicherheitsäquivalent von 10 Millionen Euro mit einer Wahrscheinlichkeit von 0,5 vollständig zu gefährden, auch wenn der Erwartungswert 30 Millionen Euro beträgt: Der Vorteil für einen mittellosen Entscheider 30 statt 10 Millionen Euro zu gewinnen wird nämlich in der Regel als viel weniger bedeutsam betrachtet, als der Nachteil, statt 10 Millionen Euro gar nichts zu gewinnen, obwohl die Differenz im ersten Fall mit 20 Millionen Euro doppelt so hoch ist wie die Differenz von 10 Millionen Euro im zweiten Fall.

Auch eine risikofreudige Strategie kann bei entsprechenden Rahmenbedingungen sinnvoll sein. Dies ist insbesondere der Fall, wenn ein Entscheider zwingend einen gewissen Sockelbetrag benötigt, der aber über dem Erwartungswert liegt. Beispiel: Ein mittelloser Entscheider entdeckt auf einem Flohmarkt einen sehr wertvollen Edelstein, der aus Unkenntnis des Verkäufers zu einem Preis von 10 Euro angeboten wird. Wenn dem Entscheider nun ein Spiel angeboten wird, bei dem der Erwartungswert 5 Euro beträgt, wird er dennoch versuchen, einen Gewinn von 10 Euro zu erreichen, auch wenn die Wahrscheinlichkeit eines Totalverlustes dann hoch sein sollte. Denn in Anbetracht des potenziell möglichen Edelsteinkaufs für 10 Euro spielt die drohende Möglichkeit eines Totalverlustes für den Entscheider kaum eine Rolle. Das Sicherheitsäquivalent des Entscheiders könnte hier je nach Wert des Edelsteins durchaus drei- oder sogar vierstellig sein. Entscheidend ist, dass der Entscheider den mit einem potenziellen Spielgewinn von 10 Euro unmittelbar realisierbaren weiteren, viel höheren (externen) Gewinn mittels des günstigen Edelsteinkaufs in seine Überlegungen mit einbezieht.