Tangentialebene

Der Boden bildet eine Tangentialebene zu diesen beiden Kugeln.

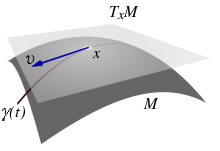
Die Tangentialebene einer Fläche ist diejenige Ebene, die im betrachteten Punkt die Fläche berührt. Sie steht senkrecht auf dem Normalenvektor der Fläche. Sie bildet den zweidimensionalen Spezialfall eines Tangentialraums einer Mannigfaltigkeit.

Definition

Veranschaulichung der Definition. Hier heißt der Berührungspunkt x, nicht p.

Es sei $M\subset\R^3$ eine reguläre Fläche und $p\in M$ ein Punkt.

• Die Tangentialebene T_pM ist die Ebene durch p, die von den Geschwindigkeitsvektoren von durch p verlaufenden Wegen aufgespannt wird: Ist die Funktion $\gamma\colon(-1,1)\to M$ ein Weg mit γ(0) = p, so ist $p + \dot\gamma(0)$ ein Punkt der Tangentialebene. Da die Tangentialebene zweidimensional ist, genügen zwei solcher Wege (in verschiedene Richtungen), um die Tangentialebene aufzuspannen.

Mit anderen Worten: Legt man zwei verschiedene Ebenen durch p, betrachtet dann deren Schnittkurven mit der untersuchten Fläche und spannt mit deren Tangenten an p eine Ebene auf, so ist dies die Tangentialebene.

Beispiel

Ist p = (x₀,y₀,z₀) ein Punkt auf dem Ellipsoid

$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1,$

so ist die Tangentialebene in p gegeben durch

$\frac{x_0x}{a^2}+\frac{y_0y}{b^2}+\frac{z_0z}{c^2}=1.$

Eigenschaften

Ist die Gauß-Krümmung der Fläche

• positiv, so liegt die Fläche in der Nähe des Berührungspunktes auf nur einer Seite der Tangentialebene; man kann sich die Fläche dann als an einem Punkt auf die Ebene aufgelegt vorstellen;
• negativ, so wird die Fläche von der Tangentialebene geschnitten.

Anwendungen

Die Tangentialebene ist eine lokale Approximation an die Fläche, die eine einfachere Struktur besitzt. Dies wird beispielsweise genutzt für:

• Abbildungen (Projektionen von Flächen auf eine Ebene, wie es etwa für Karten notwendig ist)
• vereinfachte Berechnung ebener Koordinaten in der Vermessungskunde
• Korrektur von Höhenmessungen wegen der Erdkrümmung.

Literatur

• Manfredo Perdigão do Carmo: Differential Geometry of Curves and Surfaces, Prentice-Hall, Inc., New Jersey, 1976, ISBN 0-13-212589-7