Teilspielperfektes Gleichgewicht

Beispiel I. Das blaue Oval um B und C markiert einen Informationsbezirk

Beispiel II

Das teilspielperfekte Gleichgewicht ist ein von Reinhard Selten entwickeltes Konzept der mathematischen Spieltheorie für Spiele in Extensivform. Es stellt eine Verfeinerung des Nash-Gleichgewichtes dar, d.h.: jedes teilspielperfekte Gleichgewicht ist auch ein Nash-Gleichgewicht.

Es stützt sich auf den Begriff des Teilspiels, der seinerseits speziell für dieses Konzept entwickelt wurde. Ein Teilspiel ist ein Spiel, das in einem einzelnen Entscheidungsknoten des Spielbaums beginnt und alle Knoten enthält, die diesem Knoten nachfolgen. Überdies dürfen durch das Teilspiel keine nachfolgenden Informationsbezirke zertrennt werden. Somit enthält jedes extensive Spiel zumindest ein Teilspiel, nämlich sich selbst. Echte Teilspiele, also weitere Teilspiele neben dem Spiel selbst, sind jedoch auch bei komplexen Spielen nicht garantiert.

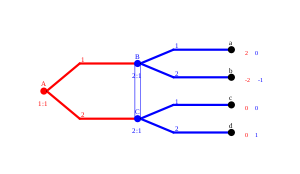
Beispiel I enthält kein echtes Teilspiel, Beispiel II hingegen zwei: Ein in Knoten B beginnendes und ein in Knoten C beginnendes.

Ein Nash-Gleichgewicht ist teilspielperfekt, wenn es ein Nash-Gleichgewicht in jedem Teilspiel von G induziert.

Jedes teilspielperfekte Gleichgewicht stellt gleichzeitig das Strategieprofil für ein sequentielles Gleichgewicht dar.

Beispiel I hat ein Nashgleichgewicht, in dem die Spieler jeweils eine gemischte Strategie verwenden. Da es nur sich selbst als Teilspiel hat, ist das Gleichgewicht trivial teilspielperfekt.

Beispiel II hat die Gleichgewichte (1/(1/1)); (1/(1/2)) und (2/(2/2)). (2/(2/2)) ist jedoch nicht teilspielperfekt, da bei Erreichen von B für das verbleibende Teilspiel kein Gleichgewicht induziert wird bzw. würde. Die Strategie (2/2) (vor dem Spiel) zu annonzieren würde Spieler 2 zwar eine höhere Auszahlung bescheren, wenn diese Ankündigung von Spieler 1 geglaubt würde, die damit verbundene Drohung (auf 2 mit 2 zu reagieren) ist jedoch unglaubwürdig.

"Glaubwürdig" ist in dieser Theorie eine Ankündigung eines Spielers i, auf eine mögliche Situation s mit einer Aktion a zu antworten genau dann, wenn a gegeben s den Nutzwert des i maximiert. Da im Beispiel II der Spieler 2 gemäß Strategie (2/2) in Situation B nicht mit dem nutzenmaxierenden Zug 1, sondern mit Zug 2 antworten würde, wären die Ankündigung dieser Aktion "Zug 2 gegeben B" sowie der zugehörigen Strategie (2/2) "unglaubwürdig".

Common belief ist eine Aussage p für Agenten i und j genau dann wenn: i und j glauben, dass p (wahr ist) sowie i und j glauben, dass i und j glauben, dass p, sowie i und j glauben, dass i und j glauben, dass p, etc.

Wenn Spieler 1 glaubt, dass die Rationalität von Spieler 1 und Spieler 2 common belief ist und glaubt, dass die Akzeptanz des Konzeptes Teilspielperfektion unter rationalen Spielern common belief ist und glaubt, dass alle nach Situation B in Beispiel II möglichen Auszahlungen (für beide Spieler) common belief sind, dann: ist in Beispiel II die Ankündigung von Strategie (2/2) und insbesondere die Androhung von Zug 2 des Spielers 2 gegeben Situation B (Zug 1 des Spielers 1) für diesen Spieler 1 im Wortsinne unglaubwürdig. Zudem glaubt Spieler 1 dann auch, dass diese Unglaubwürdigkeit unter rationalen Spielern common belief ist.

Der Sinn dieses Gleichgewichtskonzeptes ist, dass das Verhalten rationaler Spieler nicht auf unglaubwürdigen Ankündigungen beruhen darf. Beispiel: Ein Monopolist droht einem potenziell in den Markt eintretenden Konkurrenten damit, ihn durch einen aggressiven Preiskampf zu ruinieren, wenn er in den Markt eintritt. Dieser Preiskampf würde aber auch den Monopolisten stärker schaden als wenn er eine Schmälerung des Gewinns hinnähme. Dann ist die Drohung des Monopolisten unglaubwürdig. Ein potenzieller Konkurrent sollte sich dann von der Ankündigung, dass im Fall des Teilspiels "Markteintritt" die Strategie "aggressiver Preiskampf" gespielt wird, nicht beeindrucken lassen, da dies keine gleichgewichtige (Nash-) Strategie ist. Da alle Spieler dies wissen, kann ihr Verhalten nicht auf ungleichgewichtigen Ankündigungen in irgendeinem Teilspiel beruhen. Damit schließt Teilspielperfektheit ggf. unplausible Nash-Gleichgewichte aus.

Allerdings: Angenommen, dass rationale Spieler nie Ankündigungen machen würden, von denen sie glauben, dass ihre Unglaubwürdigkeit common belief ist. Wenn nun, in Beispiel II der Spieler 2 (vor der Partie) doch die Ankündiungung machen sollte, auf Zug 1 (von Spieler 1) mit Zug 2 zu antworten, dann wäre diese Ankündigung zwar unglaubwürdig - doch dann hätte Spieler 1 Probleme, diese Ankündigung zu interpretieren, sofern er Spieler 2 bis dahin für rational gehalten hatte.