- Lösungskonzepte (Spieltheorie)
-
Als Lösungskonzepte kann man in der Spieltheorie Kriterien bezeichnen, die das Verhalten der Agenten erklären. Problematisch ist hierbei, dass, normativ, sehr einfache Annahmen über das menschliche Verhalten getroffen werden müssen. Die Ergebnisse der Experimentellen Wirtschaftsforschung weichen oft erheblich von den Vorhersagen der gemeinhin akzeptierten Lösungskonzepte ab.
Inhaltsverzeichnis
Dominanz
Dominanz ist das schärfste Kriterium. Man unterscheidet zwischen starker und schwacher Dominanz.
- Eine Handlungsoption si für Spieler i ist stark dominant, wenn für alle Alternativen si' und alle möglichen Gegenantworten s * gilt: Die Option si bringt für Spieler i einen größeren Nutzen als die Alternative si', d.h. ui(si,s * ) > ui(si',s * ).
- Eine Handlungsoption si für Spieler i ist schwach dominant, wenn für alle Alternativen si' und alle möglichen Gegenantworten s * gilt: Die Option si bringt für Spieler i einen mindestens so großen Nutzen wie die Alternative si', d.h.
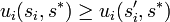 , und für mindestens eine Antwort s * gilt die strenge Ungleichung ui(si,s * ) > ui(si',s * ).
, und für mindestens eine Antwort s * gilt die strenge Ungleichung ui(si,s * ) > ui(si',s * ).
In einem Spiel können mehrere schwach dominante Strategien existieren, während eine stark dominante Strategie, wenn sie existiert, stets eindeutig ist.
Unter den in der Spieltheorie üblichen Annahmen folgt, dass rationale, nur an ihrem eigenen Wohl interessierte Spieler eine dominante Lösung spielen würden.
In quasilinearer Umgebung implementieren die Vickrey-Clarke-Groves-Mechanismen effiziente Lösungen in schwach dominanten Strategien.
Nash-Gleichgewicht
Das Nash-Gleichgewicht ist nach einem der Nobelpreisträger des Jahres 1994, John Nash benannt, der dieses Kriterium etabliert hat. Ein Nash-Gleichgewicht ist eine Kombination von Strategien, bei der die Strategie eines jeden Spielers optimal ist bezüglich der Strategien der Gegner. In der Regel werden dabei auch so genannte gemischte Strategien berücksichtigt, bei denen mehrere reine Strategien mit einer positiven Wahrscheinlichkeit gespielt werden. Ist ein Spiel durch Dominanz lösbar, so ist die dominante Lösung gleichzeitig ein Nash-Gleichgewicht (Beweis trivial).
Mächtig ist dieses Lösungskonzept, da gezeigt werden kann, dass für eine große und wichtige Klasse von Spielen, unter anderem für alle Spiele mit endlicher Zahl von Spielern und Strategien, mindestens ein Nashgleichgewicht in gemischten Strategien existiert. Problematisch ist, dass dieses Konzept nur in Ausnahmefällen eine eindeutige Lösung bietet, meist lässt es mehrere Strategiekombinationen als Lösungen zu, manchmal alle.
Verfeinerungen des Nash-Gleichgewichtes
Lässt das Nash-Gleichgewicht mehrere Lösungen zu, so kommen Verfeinerungen zum Zug. Diese sind: Perfektion, die gegen suboptimales gegnerisches Verhalten schützt. Dieses Konzept wurde durch Reinhard Selten, ebenfalls Nobelpreisgewinner 1994, in die Debatte eingebracht; Striktheit, die fordert, dass ein Gleichgewicht strikt besser ist als seine unmittelbare Umgebung; Risikodominanz; Pareto-Effizienz gegenüber allen anderen Nash-Gleichgewichten, Evolutionäre Stabilität.
Speziell für die Extensivform gibt es das Teilspielperfekte- und das Sequentielle Gleichgewicht.
Lösungen für kooperative Spiele
Für die Kooperative Spieltheorie hat man eigene Lösungskonzepte entwickelt. Unter anderem Imputationsmenge, Nucleolus, Nash-Verhandlungslösung, Kalai-Smorodinski-Lösung, den Shapley-Wert oder die Mean-Voter-Lösung.
Maximin-/Minimax-Lösung
Mit der Maximin-Lösung konnte man Zweipersonen-Einsummenspiele bereits befriedigend lösen, bevor sich das Nash-Kriterium etablierte, da in dieser Klasse die Max-Min-Lösung ein Nash-Gleichgewicht ist. Doch auch für Vielsummenspiele kommt manchmal diese Lösung in Betracht, obwohl sie in diesem Fall keine Optimalität gewährleistet, da sie manchmal weniger riskant als das Nash-Gleichgewicht ist.
Bayessches Nash-Gleichgewicht
In einem Bayesschen Spiel sind die Spielerpräferenzen private Information der Teilnehmer. Zur Berechnung der optimalen Strategie treffen die Spieler daher Annahmen der Art, dass die unbekannten Präferenzen der anderen Spieler sich als zufällige Größen mit bekannter Wahrscheinlichkeitsverteilung darstellen lassen. Die strategisch zu optimierende Größe ist dann der erwartete Nutzen einer Handlungsoption. Ein Bayessches Nash-Gleichgewicht ist ein Nash-Gleichgewicht bezüglich des Bayesschen Spieles.
Weblinks
- Gambit - eine umfangreiche Spieltheoriesoftware unter der GPL
- Spieltheorie-Software.de - Eine Software, programmiert in Java, zum Spielen und zur umfangreichen Analyse von 2-Personen Spielen
Wikimedia Foundation.
