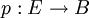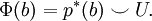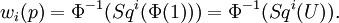Thom-Komplex

Der Thom-Raum oder Thom-Komplex, benannt nach René Thom, ist in der algebraischen Topologie und Differentialtopologie ein einem Vektorbündel zugeordneter topologischer Raum.

Ein k-dimensionales reelles Vektorbündel E über einem parakompakten Raum B sei durch

$p:E \to B$

gegeben. Dann ist für jeden Punkt b der Basis B die Fiber F_b des Vektorbündels ein k-dimensionaler reeller Vektorraum. Ein zugehöriges Sphären-Bündel Sph(E) → B kann durch separate 1 Punkt-Kompaktifizierung jeder Fiber gebildet werden. Aus dem Bündel Sph(E) erhält man den Thom-Komplex T(E) indem alle neu hinzugefügten Punkte mit dem Punkt $\infty$ identifiziert werden, dem Basispunkt von T(E).

Die Bedeutung dieser Konstruktion ergibt sich aus folgendem Satz aus der Kohomologie der Faserbündel (hier in Z₂ Kohomologie formuliert, um Komplikationen aus Orientierbarkeitsfragen zu vermeiden).

B, E, und p seien wie oben definiert. Dann gibt es einen Isomorphismus, den Thom-Isomorphismus

$\Phi \colon H^i(B; \mathbf{Z}_2) \to \tilde{H}^{i+k}(T(E); \mathbf{Z}_2)$,

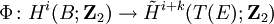für alle i größer oder gleich 0, wobei die rechte Seite die reduzierte Kohomologie ist.

Der Satz lässt sich geometrisch so interpretieren: Da E ein Vektorbündel ist, ist es auch eine Retraktion auf den Basisraumis B. Der Satz drückt aus, dass in gewisser Weise auch die Kohomologiegruppen von E zu denen von B äquivalent sind.

Der Satz wurde von René Thom in seiner Dissertation 1952 bewiesen. Er gab auch eine explizite Konstruktion des Thom-Isomorphismus. Dieser bildet das identische Element von H*(B) auf eine Klasse U in der k-ten Kohomologiegruppe des Thom-Raumes ab, die Thom-Klasse. Damit kann man für eine Kohomologieklasse b in der Kohomologie des Basisraums den Isomorphismus über den pullback der Bündel-Projektion und das kohomologische Cup-Produkt berechnen:

$\Phi(b) = p^*(b) \smile U.$

Thom zeigte in seiner Arbeit von 1954 weiter, dass die Thom-Klasse, die Stiefel-Whitney-Klassen und die Steenrod-Operationen miteinander verbunden sind. Weiter zeigte er, dass die Kobordismengruppen als Homotopiegruppen bestimmter Räume MSO(n) berechnet werden können, die selbst als Thom-Räume konstruiert werden können. Sie bilden im Sinne der Homotopietheorie ein Spektrum MSO, genannt Thom-Spektrum. Das war ein wichtiger Schritt zur modernen stabilen Homotopietheorie.

Falls Steenrod-Operationen definiert werden können, kann man mit ihnen und dem Isomorphismus Stiefel-Whitney-Klassen konstruieren. Nach Definition sind die Steenrod-Operationen (mod 2) natürliche Transformationen

$Sq^i \colon H^m(-; \mathbf{Z}_2) \to H^{m+i}(-; \mathbf{Z}_2)$,

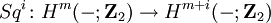definiert für alle natürlichen Zahlen m. Falls i = m ist, stimmt Sqⁱ mit dem Quadrat des Cup überein. Die iten Stiefel-Whitney-Klassen w_i (p) des Vektorbündels p : E → B sind dann gegeben durch:

$w_i(p) = \Phi^{-1}(Sq^i(\Phi(1))) = \Phi^{-1}(Sq^i(U)).\,$

Literatur

• Dennis Sullivan, René Thom's Work on Geometric Homology and Bordism. Bull. Am. Math. Soc. Bd.41, 2004, S. 341-350, online hier:[1]
• Rene Thom Espaces fibres en spheres et carres de Steenrod, Ann.Ecole Normale Superieure, Bd.60, 1952, online hier [2]
• René Thom, Quelques propriétés globales des variétés differentiables. Comm. Math. Helv. Bd. 28 (1954), S. 17-86, online hier:[3]
• J.P. May, A Concise Course in Algebraic Topology. University of Chicago Press, 1999, S. 183-198.