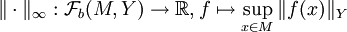Tschebyschew-Norm

Unter der Supremumsnorm versteht man in der Analysis, einem Teilgebiet der Mathematik, eine Norm auf einem Funktionenraum.

Formale Definition

Sei M eine nichtleere Menge, 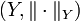$(Y, \|\cdot\|_Y)$ ein normierter Raum und 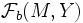$\mathcal F_b(M, Y)$ der Funktionenraum der beschränkten Funktionen von M nach Y.

Dann wird durch

$\|\cdot\|_\infty: \mathcal F_b(M, Y) \rightarrow \mathbb R, f \mapsto \sup_{x \in M}\|f(x)\|_Y$

eine Norm auf 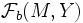$\mathcal F_b(M, Y)$ definiert.

Hierbei ist es wichtig, dass die Funktionen beschränkt sind, weil das Supremum sonst unendlich wird.

Der Raum 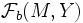$\mathcal F_b(M, Y)$ wird auch als 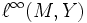$\ell^\infty(M,Y)$ bezeichnet.

Eigenschaften

• Ist der Bildraum vollständig, also ein Banachraum, so ist es auch der gesamte Funktionenraum $\mathcal F_b(M, Y)$.
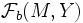• Ist M nicht endlich, so ist nicht jede abgeschlossene, beschränkte Teilmenge von 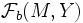$\mathcal F_b(M, Y)$ automatisch kompakt.
• Ist M nicht endlich, so ist 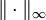$\|\cdot\|_\infty$ nicht zu allen Normen auf 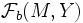$\mathcal F_b(M, Y)$ äquivalent.
• Ist der Zielraum 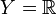$Y=\mathbb{R}$, dann lassen sich Funktionen in 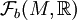$\mathcal F_b(M, \mathbb{R})$ nicht nur punktweise addieren, sondern auch multiplizieren. Die Supremumsnorm ist dann submultiplikativ, d.h. 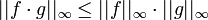$||f\cdot g||_\infty \leq ||f||_\infty\cdot ||g||_\infty$. Der Raum 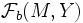$\mathcal F_b(M, Y)$ wird mit der punktweisen Multiplikation zu einer Banachalgebra.

Siehe auch

• Metrischer Raum
• Maximumsnorm
• Funktionenraum
• Normierter Raum
• Kompakter Raum
• Folge
• Wesentliches Supremum