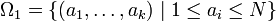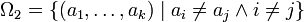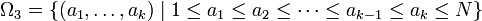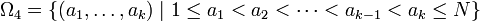Uneingeschränkte Zufallsstichprobe

Ein Urnenmodell beschreibt ein hypothetisches Experiment und stellt eine Form der Zufallsstichprobe dar. Dazu wird ein fiktives Gefäß mit Kugeln gefüllt, welche anschließend zufällig gezogen werden. Durch ein Urnenmodell lassen sich so verschiedene Zufallsexperimente, etwa eine Lottoziehung, simulieren.

Voraussetzung für die Anwendung des Urnenmodells ist das Vorliegen eines Laplaceschen Wahrscheinlichkeitsraumes. Der Stichprobenraum Ω ist hierbei endlich und mit der Gleichverteilung versehen. Der Ereignisraum Σ wird somit gegeben durch 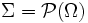$\Sigma = \mathcal{P} ( \Omega )$, die Potenzmenge von Ω.

Das Urnenmodell dient zur Vereinfachung der Lösung kombinatorischer Abzählprobleme, die man bei der Betrachtung von Laplace-Wahrscheinlichkeitsexperimenten häufig antrifft.

Konkretisierung der Modelle

In die Urne werden N durchnummerierte Kugeln gegeben. Anschließend k Kugeln aus der Urne zufällig gezogen.

Zusätzlich ist festzulegen, ob eine gezogene Kugel wieder in die Urne zurückgelegt werden soll, oder außerhalb der Urne verbleibt. In letzterem Fall können natürlich nicht mehr Kugeln gezogen werden, als in der Urne zu Beginn waren ($k \leq N$).

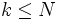Weiter ist zu beachten, ob man nur an der "Gesamtheit" aller gezogenen Kugeln interessiert ist, oder ebenso an ihrer Reihenfolge. Die Reihenfolge der Kugeln wäre beispielsweise wichtig, wenn sich daraus eine Telefonnummer ergäbe. Unwichtig hingegen, würde sie eine Lottoziehung beschreiben. Hier kommt es bei einer gezogenen Zahl eben nicht genau darauf an, wann die Ziehung erfolgte.

Zusammenfassend lässt sich eine Ziehung durch folgende Regeln charakterisieren: von 1 bis N sonst gleichartigen Kugeln werden k aus einer Urne zufällig gezogen, wobei

• Modell 1: Ziehung in geordneter Reihenfolge, mit Zurücklegen
• Modell 2: Ziehung in geordneter Reihenfolge, ohne Zurücklegen
• Modell 3: Ungeordnete Ziehung, mit Zurücklegen
• Modell 4: Ungeordnete Ziehung, ohne Zurücklegen

beschreibt.

Mathematischer Rahmen

Stellt a_i das Ergebnis der Ziehung im Schritt i dar, so können die Ergebnisräume obiger Modelle beschrieben werden als die Mengen

• $\Omega_1 = \{(a_1, \ldots , a_k) \mid 1 \le a_i \le N\}$
• $\Omega_2 = \{(a_1, \ldots , a_k) \mid a_i \ne a_j\wedge i \ne j \}$
• $\Omega_3 = \{(a_1, \ldots , a_k) \mid 1 \leq a_1 \leq a_2 \leq \dotsb \leq a_{k-1} \leq a_k \leq N \}$
• $\Omega_4 = \{(a_1, \ldots , a_k) \mid 1 \leq a_1 < a_2 < \dotsb < a_{k-1} < a_k \leq N \}$

Um nun Aussagen über Wahrscheinlichkeiten treffen zu können, möchte man die Mächtigkeit der Ω_i bestimmen:

• | Ω₁(N,k) | = N^k
• $| \Omega_2 (N,k) | = {N \choose k} \cdot k!$
• $| \Omega_3 (N,k) | = {N+k-1 \choose k}$
• $| \Omega_4 (N,k) | = {N \choose k}$

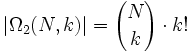
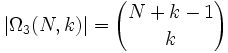
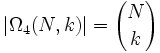
Wobei ${N \choose k} = \frac{ N! }{ (N-k)! k! }$

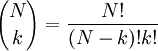
Beispiel

• Wie groß ist beim Zahlenlotto (6 aus 49) die Wahrscheinlichkeit P für 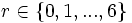$r \in \lbrace 0,1,...,6 \rbrace$ Richtige?

Verwende das Modell Ω₄ mit Ziehung ohne Zurücklegen, ohne Berücksichtigung der Reihenfolge:

$P = \frac{ | \Omega_4 (6,r) | \cdot | \Omega_4 (43,6-r) | }{ | \Omega_4 (49,6) | }$ $= \frac{ {6 \choose r} \cdot {43 \choose 6-r} }{ {49 \choose 6} }$

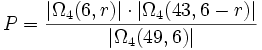
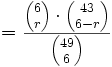
Anschaulich bedeutet dies:

$| \Omega_4 (6,r) |=[\mathrm{ Anzahl\,der\,M \ddot o glichkeiten\,\,r\,von\,6\,\,gezogenen\,Zahlen\,zu\,w \ddot a hlen}]$

$| \Omega_4 (43,6-r) | = [\mathrm{ Anzahl\,der\,M \ddot o glichkeiten\,\,(6-r)\,von\,43\,\,nicht\,gezogenen\,Zahlen\,zu\,w \ddot a hlen}]$

$| \Omega_4 (49,6) | = [\mathrm{Anzahl\,aller\,M \ddot o glichkeiten\,bei\,der\,Ziehung\,von\,6\,aus\,49}]$

Hierbei muss man beachten, dass die Wahrscheinlichkeit für alle Ereignisse aus Ω₄ gleich groß ist.

• Beim Modell Ω₃ liegt keine Gleichverteilung vor:

Zieht man aus einer Urne mit 2 Kugeln 2 mal mit Zurücklegen und ohne Berücksichtigung der Reihenfolge erhält man: Die Wahrscheinlichkeit, zwei mal die erste Kugel zu ziehen ist ein Viertel, die Wahrscheinlichkeit, zwei mal die zweite Kugel zu ziehen ebenfalls, aber man zieht mit Wahrscheinlichkeit ein Halb zwei verschiedene Kugeln.

Literatur

• Gerd Fischer: Stochastik einmal anders ISBN 3-528-03967-1
• Norman L. Johnson, Samuel Kotz: Urn Models and Their Application. New York: John Wiley & Sons 1977, ISBN 0471446300

Weblinks

• Urnenmodell Modellierungsbeispiele.
• Urnenmodell-Erklärung Einfache Herleitung und Beispiele.