Varianzschätzer

In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: In diesem Artikel wird als einzige Varianzschätzung die korrigierte Stichprobenvarianz erwähnt. Es fehlen konkrete Verfahren zur Schätzung der Varianz, die auf den gelisteten allgemeinen statistischen Methoden beruhen. Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Varianzschätzung ist in der Statistik die Schätzung einer unbekannten Varianz der Grundgesamtheit. Sie ist eine Methode zur Messung der Genauigkeit von Schätzverfahren, da die Varianz von Schätzverfahren ein Genauigkeitsmaß darstellt. Die Varianz wird bei einfacher Zufallsauswahl durch die Stichprobenvarianz geschätzt (korrigiert um 1/n-1). Bei komplexen Stichprobenverfahren sind andere Varianzschätzer anzuwenden. Die Methoden werden angewendet, um Konfidenzintervalle angeben zu können. Die Varianzschätzer können von Schätzern für Totalwerte abgeleitet werden.

Analytische Methoden

Direkte Verfahren - Lineare Schätzer

Bei direkten Methoden lässt sich die Varianz explizit darstellen. Sie lassen sich meist nur bei einfachen Punktschätzern angeben. Hier werden Approximationsformeln nur bei Stichprobendesigns mit Inklusionswahrscheinlichkeiten zweiter Ordnung benötigt. Exakte Methoden, das heißt einfach auszurechnende Formeln können im Fall eines Linearen Schätzers angegeben werden. Dies ist generell möglich bei Zufallsauswahlen.

• Uneingeschränkte Zufallsstichprobe: Für die Varianz (σ²) der Grundgesamtheit verwendet man zumeist die korrigierte Stichprobenvarianz 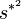$s^{*^{2}}$ als Schätzfunktion:

$\widehat{varX}= S^{*^{2}}= \frac{1}{n-1}\sum_{i=1}^n (X_i- \bar X)^2$ .

• Mehrstufige Zufallsstichproben (Schichtung)

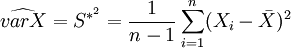Schätzung der Varianz einer Normalverteilung

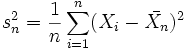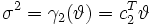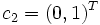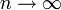Der Maximum-Likelihood-Schätzer $s_n^2 = \frac 1n \sum_{i=1}^{n} (X_i - \bar{X_n})^2$ ist dagegen nicht erwartungstreu für $\sigma^2 = \gamma_2(\vartheta) = c_2^T \vartheta \;$ mit $c_2 = (0,1)^T\;$, da sich $E[s_n^2] = \frac{n-1}{n} \sigma^2\;$ zeigen lässt. Der Bias beträgt also $E[s_n^2] - \sigma^2 = -\frac{1}{n} \sigma^2.\;$ Da dieser asymptotisch, also für $n \rightarrow \infty\;$, verschwindet, ist der Schätzer allerdings asymptotisch erwartungstreu.

Linearisierungsmethoden - Nicht-Linearer Schätzer

Bei nicht-linearen Schätzern (z.B. einem Ratio-Schätzer) kommen approximative Methoden zum Einsatz. Unter anderem untersucht man Schätzungsgleichungen und Einflussfunktionen. Durch die Woodruff-Linearisierung können nicht lineare Schätzer zu linearen umgewandelt werden. Eine weitere Methode ist die Taylorapproximation.

Beispiele:

• Verallgemeinerter Regressionsschätzer
• Residualvarianzschätzer

Resampling-Methoden

Ist dies auch nicht möglich, kommen Resamplingmethoden zum Einsatz. Dazu werden Substichproben der eigentlichen Stichprobe mit n Elementen gezogen. Bei der Schätzung kann dann das Stichprobendesign durch Gewichtung berücksichtigt werden.

Resampling-Methoden:

• Random Groups
• Balanced Repeated Replication
• Jackknife-Methoden
• Bootstrap-Methoden

siehe zu "Varianzschätzung mit Mikrozensusdaten unter Berücksichtigung des Stichprobendesigns" den Artikel bei GESIS

Siehe auch

Mittelwertschätzung

Weblinks

Anwendungsbeispiel

Literatur

• Stenger, Horst: Varianzschätzung bei komplexen Stichprobenerhebungen. In: Aktuelle Probleme und neue Methoden der Verkehrsstatistik. Hrsg.: Hautzinger, H.. Bergisch Gladbach: DVWG, 1985, S. 143-150
• Davison, A.; Hinkley, D.V. (2003): Bootstrap methods and their application.
• Davison, A.; Sardy, S. (2004): DACSEIS reports D5.1 and D5.2.
• Wolter, K. (1985): Introduction to variance estimation.
• Strauss, Ingo (1979): Zulässigkeit von Varianzschaetzungen in der Stichprobentheorie
• Vollmerhaus, Rainer (1989): Robuste Schätzung der Varianz