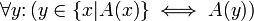Unmenge

Mit Klasse wird heute in der Mathematik, Klassenlogik und Mengenlehre eine Zusammenfassung von Objekten bezeichnet. Eine Klasse wird definiert durch eine logische Eigenschaft, die alle Objekte der Klasse erfüllen.

In der Mathematik des 19. Jahrhunderts wurden die Begriffe „Klasse“ und „Menge“ weitgehend synonym verwendet und waren ungenügend festgelegt, so dass widersprüchliche Interpretationen möglich waren. Im 20. Jahrhundert wurden sie im Zuge der Axiomatisierung der Mengenlehre getrennt und nach und nach präzisiert. Der Begriff „Klasse“ ist dann umfassender als der Begriff „Menge“. Klassen unterliegen keinen Einschränkungen in ihrer Bildung oder Definition. Sie dürfen aber nur eingeschränkt verwendet werden, damit nicht die Widersprüche der naiven Mengenlehre entstehen. Nur ein unsachgemäßer Umgang mit Klassen ist daher problematisch.

Ein speziellerer Klassenbegriff liegt bei Äquivalenzklassen vor. Hier handelt es sich um eine Zerlegung einer Klasse oder Menge in disjunkte Teilklassen oder Teilmengen.

Definitionen

Ist 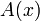$\,A(x)$ eine beliebige logisch korrekt gebildete Aussage mit der Variablen 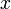$\,x$, so bezeichnet 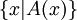$\,\{x|A(x)\}$ die Klasse aller Objekte 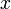$\,x$, die diese Aussage erfüllen.

Klassen in dieser Darstellung und Schreibweise werden in der Mathematik-Praxis heute überall verwendet, unabhängig davon, welche axiomatische Grundlage vorausgesetzt wird. Für ihre Anwendung ist es also nicht entscheidend, ob die Zermelo-Fraenkel-Mengenlehre (ZF) oder die Neumann-Bernays-Gödel-Mengenlehre (NBG) oder ein anderes Axiomensystem zugrunde gelegt wird. In ZF und NBG sind aber Klassen {x | A(x)} keine offiziellen Terme, sondern werden nur zur praktischen Darstellung benutzt; dort liegt also genau genommen eine metalogische Klassenschreibweise vor. Erst durch zusätzliche Axiomenschemata werden sie in die logische Sprache korrekt einbezogen, zum Beispiel durch das Abstraktionsprinzip, das in ZF in folgender Form ergänzt werden kann:^[1]

$\forall y\colon (y \in \{x|A(x)\} \iff A(y))$

Dieses Abstraktionsprinzip wird in der mathematischen Praxis ständig gebraucht. Die moderne Klassenlogik berücksichtigt diese Praxis und etabliert Klassenterme in ihrer logischen Sprache. Dort besagt aber ein Klassenterm gar nichts über die Existenz einer Klasse! Die Klassenlogik ist vielmehr nur ein syntaktisch reichhaltiger logischer Rahmen, der eine bequemere optimierte Darstellung erlaubt und es gestattet, beliebige Klassen in jeden Kontext einzusetzen ohne Gefahr eines Widerspruchs.

Mengen sind im Vergleich zu den Klassen nicht eindeutig klar definiert, sondern abhängig von gewählten Mengenaxiomen. Zunächst gilt immer: Jede Menge ist auch eine Klasse, aber wegen der Widersprüche der naiven Mengenlehre sind nicht alle Klassen auch Mengen. Klassen, die keine Mengen sind, heißen echte Klassen. Das heißt, echte Klassen erfüllen gewisse Axiome der Mengenlehre nicht, wobei meist die Axiome der Zermelo-Fraenkel-Mengenlehre (ZF) gemeint sind, aber prinzipiell auch andere axiomatische Mengenlehren in Frage kommen. Zu den echten Klassen gehören insbesondere alle Klassen, die kein Element einer anderen Klasse oder Menge sein können, da zur Menge x immer die Menge {x} gebildet werden kann.

Beispiele für echte Klassen

• Die Klasse aller Objekte, die sogenannte Allklasse. In der Mengenlehre ist dies die Klasse aller Mengen.
• Die Klasse aller Mengen, die sich nicht selbst als Element enthalten, die sogenannte Russellsche Klasse.
• Die Klasse aller Gruppen.
• Die Klasse aller Ordinalzahlen.
• In bestimmten Kategorien ist die Klasse der Objekte eine echte Klasse.
• Die Klasse der surrealen Zahlen. Diese hat alle Eigenschaften eines Körpers, außer der Eigenschaft, eine Menge zu sein.
• Die Klasse aller einelementigen Mengen.
• Quine-Individuen mit {x} = x. ^[2] Sie verletzen in der Mengenlehre das Fundierungsaxiom.

Anmerkungen

Informell kann man sagen, dass eine Klasse echt ist, wenn sie „zu groß“ ist, um eine Menge zu sein (daher spricht man auch inoffiziell von „Unmengen“ in Anspielung auf die umgangssprachliche Bedeutung einer unüberschaubaren Menge). So ist etwa die Klasse aller ganzen Zahlen eine Menge – zwar unendlich groß, aber doch handhabbar; die Klasse aller Gruppen hingegen, sowie die Klasse aller Mengen, sind „zu groß“ und daher echte Klassen. Die Umkehrung, dass echte Klassen immer zu große Klassen sind, gilt nicht, denn es gibt in gewissen Mengenlehren auch kleine echte Klassen, wie das letzte Beispiel belegt.

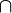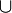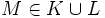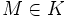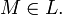Echte Klassen unterliegen nicht den Mengenaxiomen. Klassen können aber mit denselben Operationen wie Mengen verknüpft werden, etwa mit $\cap\!\,$ und $\cup\!\,$. Für diese beiden Operationen gelten auch dieselben Sätze, etwa $M\in K\cup L$ genau dann, wenn $M\in K$ oder $M\in L.$. Auch andere Mengen-Operationen sind mit Klassen möglich, aber es gelten dann oft nicht alle in der Mengenlehre beweisbaren Sätze. Zum Beispiel verletzt die Potenz der Allklasse Cantors zweites Diagonalargument für Potenzmengen; diese Cantorsche Antinomie nützte Cantor zum indirekten Beweis dafür, dass die Allklasse keine Menge, sondern eine echte Klasse ist. Auch andere Paradoxa der naiven Mengenlehre beweisen indirekt, dass eine bestimmte Klasse echt ist: So wird das Burali-Forti-Paradoxon ein Beweis für die Echtheit der Klasse aller Ordinalzahlen und die Russellsche Antinomie ein Beweis für die Echtheit der Russellsche Klasse.

In der Zermelo-Fraenkel-Mengenlehre sind alle realen, existenten Objekte Mengen; echte Klassen sind hier höchstens als nominelle Terme nutzbar. Dagegen sind die realen Objekte der Neumann-Bernays-Gödel-Mengenlehre Mengen und echte Klassen: Mengen sind dort alle Klassen, die Elemente anderer Klassen sind, und echten Klassen sind dort genau die Nichtelemente. Wie erwähnt, ist in NBG und ZF die Klassenschreibweise noch metalogisch, solange sie - was üblich ist - auf einer Prädikatenlogik ohne Klassenterm {x | A(x)} aufbauen; denn dieser Term ist dort auch nicht korrekt definierbar. Wählt man aber eine Klassenlogik als Basis, dann wird {x | A(x)} zum Term, mit dem beliebige Klassen gebildet werden können; diese Möglichkeit nutzt die Oberschelp-Mengenlehre als Erweiterung von ZF. Sie ist eine moderne Weiterentwicklung der Quine-Mengenlehre, die {x | A(x)} als virtuelle Klasse einsetzt, das heißt nicht als Term, sondern als Teilformeln in festgelegten Kontexten wie dem Abstraktionsprinzip.^[3]

Einzelnachweise

1. ↑ Arnold Oberschelp: Allgemeine Mengenlehre, 1994, S. 35. Oben syntaktisch vereinfacht mit gebundener Variable notiert
2. ↑ Quine, Willard Van Orman: Mengenlehre und ihre Logik, Braunschweig 1973, S. 24
3. ↑ Quine, Willard Van Orman: Mengenlehre und ihre Logik, Braunschweig 1973, S. 12

Literatur

• Arnold Oberschelp: Allgemeine Mengenlehre, Mannheim/Leipzig/Wien/Zürich, 1994, ISBN 3-860-25451-0.