Vergrößerung (Optik)

Die Vergrößerung eines optischen Instruments ist das Verhältnis zwischen der scheinbaren Größe (Größe des Bilds) und der wahren Größe eines Objekts.

• Bei optischen Instrumenten mit Einblick in ein Okular ist unter „Größe“ der Sehwinkel (Betrachtungswinkel) zu verstehen, man spricht dann von Winkelvergrößerung.
• Erscheint das Bild auf einem Schirm, ist die „Größe“ ein Längenmaß und kann mit einem Lineal gemessen werden, man spricht dann von linearer Vergrößerung. Die Vergrößerung in Richtung quer zur optischen Achse wird Lateralvergrößerung genannt, die Vergrößerung längs der optischen Achse, die für die Schärfentiefe maßgeblich ist, heißt Axialvergrößerung.

In all diesen Fällen ist die Vergrößerung eine dimensionslose Zahl, hat also keine physikalische Einheit.

Winkelvergrößerung

Die Vergrößerung V (manchmal auch Γ genannt) eines optischen Instruments, in das man mit dem Auge blickt, ist per Definition:

Sehwinkel

$V = \frac{\tan \varepsilon}{\tan \varepsilon_0}$

$\varepsilon_0$ ist der Sehwinkel unter dem man einen Gegenstand G ohne optische Hilfsmittel sieht (schwarz gezeichnet). Dieser Winkel hängt vom Abstand zwischen Auge und Gegenstand ab; je näher der Gegenstand, umso größer der Sehwinkel. Bei Lupen und Mikroskopen wird daher per Konvention ein Abstand von $S := 25\,\mathrm{cm}$ angenommen, in dem man den Gegenstand ohne optische Hilfsmittel noch scharf sehen könnte (deutliche Sehweite).

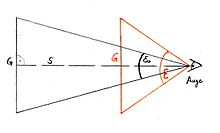
$\varepsilon$ ist der Sehwinkel, unter dem der Gegenstand im optischen Instrument erscheint (rot gezeichnet). Je größer der Sehwinkel ε, desto größer sieht das Auge den Gegenstand.

Lupe

Die Vergrößerung einer Lupe (Vergrößerungsglas) wird durch das Sehvermögen des Betrachters beeinflusst. Bei Kurzsichtigkeit ist der Wert etwas kleiner als bei Weitsichtigkeit. Daher findet man im Handel oft widersprüchliche Angaben. Damit ein nicht fehlsichtiges Auge den Gegenstand G noch entspannt sieht, darf er max. um die Brennweite f vor der Linse liegen. Die Strahlen gelangen nun parallel ins Auge. Formal errechnet sich die Vergrößerung wie folgt:

$V = \frac{ \tan\varepsilon}{ \tan\varepsilon_0} = \frac{\frac{G}{f}}{\frac{G}{25\,\mathrm{cm}}} = \frac {25\,\mathrm{cm}}{f}$

Mikroskop

Die Vergrößerung eines Mikroskops ist das Produkt aus der Vergrößerung des Objektivs V_Ob und der Vergrößerung des Okulars V_Ok.

$V = V_\mathrm{Ok} \cdot V_\mathrm{Ob}$

Die Vergrößerung des Objektivs V_Ob errechnet sich aus

$V_\mathrm{Ob}= \frac{d - f_\mathrm{Ob}}{f_\mathrm{Ob}}$,

wobei f_Ob die Brennweite des Objektivs und d der Abstand vom Objektiv zur Brennebene des Okulars ist.
Unter der Vergrößerung des Objektivs wird üblicherweise dessen Abbildungsmaßstab verstanden. Mit der Vergrößerung eines Objektivs ist also keine Winkelvergrößerung gemeint. Vorausgesetzt wird für die Berechnung, dass das Objektiv so eingesetzt wird, wie es im dazugehörenden Mikroskop vorgesehen ist. Das bedeutet, dass der Abstand zum Gegenstand so gewählt wird, dass das Zwischenbild dort entsteht, wo sich im Mikroskop die Brennebene des Okulars befindet (oder in neueren Mikroskopen eine CCD-Kamera). Die Abstände von den zwei Hauptebenen des Okulars zum Gegenstand und zum Zwischenbild sind dabei durch die Linsengleichung festgelegt.
Bei Mikroskopsystemen mit austauschbaren Objektiven wird die Verbindung der Objektive mit dem Mikroskoptubus üblicherweise so angepasst, dass die optische Tubuslänge t: = d − f_Ob, also der Abstand zwischen dem Okular-zugewandten Objektivbrennpunkt und der Zwischenbildebene, für unterschiedliche Objektive konstant bleibt. Dadurch kann die Vergrößerung des Objektivs sehr einfach berechnet werden, nämlich als

$V_\mathrm{Ob}= \frac{t}{f_\mathrm{Ob}}$

Üblich ist eine optische Tubuslänge zwischen $t = 16 \text{ und } 20\,\mathrm{cm}$.

Die Vergrößerung des Okulars ist wie die einer Lupe durch

$V_\mathrm{Ok} = {25\,\mathrm{cm}} / f_\mathrm{Ok}$

gegeben. Genauso wie die Gesamtvergrößerung eines Mikroskops entspricht sie einer Winkelvergrößerung.

Keplersches Fernrohr

Die Vergrößerung eines Fernrohrs (astronomisches Fernrohr oder Feldstecher mit Umkehrprismen) ist durch

$V= \frac{f_\mathrm{Ob}}{f_\mathrm{Ok}}$

gegeben. Dabei sind f_Ob und f_Ok die Brennweiten von Objektiv bzw. Okular.

Auch das Verhältnis von Öffnung (Objektivdurchmesser, Apertur) zur Austrittspupille des Fernrohrs ist durch die Vergrößerung gegeben. Da das Auge nicht mehr Licht erfassen kann, als durch die Pupille ins Auge gelangen kann, ergibt sich daraus eine untere Grenze der Vergrößerung (Bei einem Pupillendurchmesser des Auges von 7 mm: Objektivdurchmesser in mm dividiert durch 7). Wird diese unterschritten, wird das Lichtsammelvermögen des Fernrohrs nicht voll ausgenutzt.

Da wegen der Beugung des Lichts das Auflösungsvermögen des Fernrohrs vom Objektivdurchmesser abhängig ist, gibt es auch eine obere Grenze für die maximal sinnvolle Vergrößerung. Die Vergrößerung, welche das Auflösungsvermögen des Fernrohrs der des menschlichen Auges optimal anpasst, wird als nützliche Vergrößerung bezeichnet. Diese ist zahlenmäßig etwa so groß, wie der Durchmesser des Fernrohrobjektivs in Millimetern. Bei einer stärkeren Vergrößerung erscheinen Sterne nicht als Punkte, sondern als Scheibchen, die von konzentrischen Kreisen (Beugungsringen) umgeben sind.

Grenzen der Vergrößerung

Abbildungsfehler, Beugungserscheinungen und bei Fernrohren die Turbulenzen der Luft („Seeing“) begrenzen die maximal nutzbare Vergrößerung. Das Bild kann zwar theoretisch beliebig stark vergrößert werden, doch die Bildinformation ist begrenzt. Das Bild wird zunehmend unschärfer.