Schärfentiefe

Nur ein schmaler Bereich des Bilds erscheint scharf – ein Beispiel für geringe Schärfentiefe

Kleiner Schärfentiefebereich durch Verwendung eines lichtstarken Superteleobjektivs (4,5/500 mm)

Die Schärfentiefe ist ein Maß für die Ausdehnung des scharfen Bereichs im Objektraum eines abbildenden optischen Systems. Der Begriff spielt in der Fotografie eine zentrale Rolle und beschreibt die Größe des Entfernungsbereichs, innerhalb dessen ein Objekt hinlänglich scharf im Abbild der Kameraoptik erscheint. In der Regel wird eine große Schärfentiefe durch kleine Blendenöffnungen oder Objektive mit kurzen Brennweiten erreicht: Von vorn bis hinten sieht dann alles mehr oder weniger scharf aus. Das Gegenteil ist der sogenannte „Film-Look“, bei dem der Bereich der Schärfentiefe klein ist (englisch: shallow): Die Kamera zeichnet die zentrale Figur scharf, eventuell nur das Auge einer Person,^[1] während alles vor und hinter ihr unscharf erscheint. Tief bedeutet bei Schärfentiefe die Tiefe des Raums, also die Richtung weg von der Optik. In der Computeranimation ist die Schärfentiefe ein optischer Effekt, der im Nachhinein in jedes einzelne Bild eingerechnet wird und deshalb erheblichen Rechenaufwand bedeutet. Meist wird hier der englische Begriff Depth of Field (DOF) benutzt.^[2]

Umgangssprachlich werden Schärfentiefe und Tiefenschärfe synonym verwendet, wobei Schärfentiefe der wissenschaftlich-semantisch exaktere Begriff ist.^[3]

Geometrische Schärfentiefe

Es sind grundsätzlich zwei verschiedene Anordnungen zu unterscheiden: Die Camera obscura, die lediglich aus einer einzigen Lochblende besteht, und ein Linsensystem, das so eine Blende ebenfalls enthält, aber zusätzlich noch (mindestens) eine Linse (vor oder hinter der Blende), die eine reguläre optische Abbildung produziert.

Camera obscura

Von einem Objekt ausgehende Lichtstrahlen fallen durch die Lochblende auf die Bildebene (einen Schirm, einen Film oder einen Kamerabildsensor). Je nach Durchmesser der Blende werden aus diesen Lichtstrahlen mehr oder weniger dicke kegelförmige Lichtkörper; durch Schnitt der Bildebene mit einem Kegel entsteht auf der Ebene ein Kreis, sogenannte Zerstreuungskreise oder Unschärfekreise (Z). Sie existieren bei jeder Dimensionierung der Abstände zwischen Objekt, Blende und Bild, die Kreisgröße in der Bildebene berechnet sich nach dem Strahlensatz. Dabei ist der Einfluss des Lochblendendurchmessers einfach proportional: je größer das Loch, desto größer der Unschärfekreis. Für eine schärfere Abbildung wird ein kleineres Loch benötigt. Wird jedoch das Loch zu stark verkleinert, so wird der Bereich der geometrischen Optik verlassen und es treten die Welleneigenschaften des Lichtes in den Vordergrund. Die dabei auftretenden Beugungseffekte werden um so stärker, je kleiner das Loch ist. Hierdurch kommt es zu einer Abnahme der Schärfe. Somit gibt es für eine Camera obscura einen optimalen Lochduchmesser. Weiterhin muss bei dieser Optimierung neben den Abbildungseigenschaften auch der Umstand berücksichtigt werden, dass mit einem kleineren Lochdurchmesser der Lichtstrom abnimmt und damit die Belichtungszeiten zunehmen.

Linsensystem

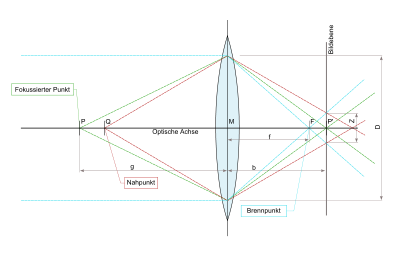
Der Aufbau mit einer zusätzlichen Linse ändert am Prinzip nur so viel, dass die Linse dafür sorgt, dass (im idealen Fall) bei einer bestimmten Entfernung der Bildebene von der Linse eine scharfe Abbildung auftritt, bei dieser Position entfällt also die obige Ungenauigkeit (und die Blendenöffnung kann im Interesse besserer Lichtausbeute wesentlich vergrößert werden). Erst wenn es um Objektpunkte geht, die vor oder hinter dieser scharf abgebildeten Position liegen, verringert sich diese Schärfe und sinkt mit wachsendem Abstand auf den Wert, den die Blende allein als Camera obscura bewirken würde. Genauer:

In der geometrischen Optik können nur diejenigen Punkte als scharfe Bildpunkte in der Bildebene (Film, Chip) wiedergegeben werden, die auf der Ebene liegen, die sich in der Gegenstandsweite zur Linse befindet. Alle anderen Punkte, die sich auf näher oder weiter entfernt liegenden Ebenen befinden, erscheinen in der Bildebene nicht mehr als Punkte, sondern als Scheibchen, sogenannte Zerstreuungskreise oder Unschärfekreise (Z).

Zerstreuungskreise entstehen, weil die von der Linse (Objektiv) auf die Bildebene (den Film) fallenden Lichtkörper Kegel sind; durch Schnitt der Bildebene mit einem Kegel entsteht auf der Ebene ein Kreis.

Eng nebeneinander liegende Punkte, die nicht in der Gegenstandsebene liegen, werden durch eng nebeneinander liegende Zerstreuungskreise abgebildet, die sich überdecken und in den Randbereichen vermischen, wodurch ein unscharfes Bild entsteht.

Der für die Akzeptanz von Schärfe maximal tolerierbare Zerstreuungskreisdurchmesser für einen Fotoapparat wird mit Z bezeichnet. Die absolute Größe des maximalen Zerstreuungskreises Z ist abhängig vom Aufnahmeformat, da sie 1/1500 der Diagonalen beträgt. Solange die Unschärfekreise nicht größer als Z werden, liegen sie unterhalb der Auflösungsgrenze des Auges, und die Abbildung wird als scharf erachtet. Dabei entsteht der Eindruck, das Bild weise nicht nur eine Schärfenebene, sondern einen Schärfebereich auf. Problematisch wird ein eingeschränkter Schärfentiefebereich auch dann, wenn die Schärfemessung nicht direkt in der Bildebene, sondern mit gesonderten Einstellscheiben oder Schärfesensoren erfolgt, da es dann durch Toleranzen in der Bildweite leicht zu Fokussierungsfehlern kommen kann.

Die folgende Tabelle veranschaulicht die maximale Größe der Zerstreuungskreise je nach Aufnahmeformat des jeweiligen Fotoapparats:

Aufnahmeformat	Abbildungsgröße	Seitenverhältnis	Bilddiagonale	Z	Normalbrennweite
1/3″-Digitalkamera-Sensor	4,4 mm × 3,3 mm	4:3	5,5 mm	3,7 µm	6,4 mm
1/2,5″-Digitalkamera-Sensor	5,3 mm × 4,0 mm	4:3	6,6 mm	4,4 µm	7,6 mm
1/1,8″-Digitalkamera-Sensor	7,3 mm  ×  5,5 mm	4:3	9,1 mm	6,1 µm	10,5 mm
2/3″-Digitalkamera-Sensor	8,8 mm  ×  6,6 mm	4:3	11,0 mm	7,3 µm	12,7 mm
(Micro) Four Thirds Sensor	17,3 mm × 13,0 mm	4:3	21,6 mm	14,4 µm	24,9 mm
APS-C-Sensor	22,2 mm × 14,8 mm	3:2	26,7 mm	17,8 µm	30,8 mm
APS-C-Sensor	23,7 mm × 15,7 mm	3:2	28,4 mm	19,2 µm	32,8 mm
APS-H-Sensor	27,9 mm × 18,6 mm	3:2	33,5 mm	22,4 µm	38,7 mm
Kleinbildformat	36 mm × 24 mm	3:2	43,3 mm	28,8 µm	50,0 mm
Digitales Mittelformat	48 mm × 36 mm	4:3	60,0 mm	40,0 µm	69,3 mm
Mittelformat 4,5  × 6	56 mm  × 42 mm	4:3	70,0 mm	46,7 µm	80,8 mm
Mittelformat 6  × 6	56 mm  × 56 mm	1:1	79,2 mm	52,8 µm	91,5 mm
Großformate	z. B. 120 mm × 90 mm	—	—	90–100 µm	—
Größere Formate	bis 450 mm × 225 mm	—	—	> 100 µm	—

Schärfentiefe berechnen

Folgende Variablen werden benötigt:

• die Objektiv-Brennweite f, zum Beispiel 7,2 mm
• die Blendenzahl k (auch Arbeitsblende genannt), zum Beispiel 5,6
• die Gegenstandsweite g (Entfernung der fokussierten Gegenstandsebene von der vorderen Prinzipalebene), zum Beispiel 1000 mm
• der Zerstreuungskreis Z, zum Beispiel 0,006 mm

Für eine Annäherung an Z kann folgende Formel mit d als Formatdiagonale des Aufnahmeformates in mm und N als Anzahl der zu unterscheidenden Punkte entlang der Diagonalen verwendet werden:

$Z = \frac{d}{N} \approx \frac{d}{1500}$

Dieser Näherung liegt die Annahme zugrunde, dass das menschliche Auge über die Bilddiagonale maximal 1500 Punkte auflösen kann, wenn der Sehabstand etwa gleich der Bilddiagonalen ist.

Hyperfokale Entfernung

Verschiedene Strahlengänge zum Bestimmen der Schärfentiefe. Es wird auf die hyperfokale Entfernung fokussiert. Der Fernpunkt liegt damit im Unendlichen.

Zuerst wird die hyperfokale Entfernung d_h vom Linsenmittelpunkt aus berechnet:

$d_h = \frac{f^2}{k \cdot Z} + f = {f \cdot \left(\frac{D}{Z}+1\right)}$, wobei D die Eintrittspupille des Objektivs ist.

Da der rechte Summand in der Regel viel größer ist als der linke, kann der rechte Summand in den Näherungsformeln vernachlässigt werden:

$d_h \approx \frac{f^2}{k \cdot Z} = {f \cdot \frac{D}{Z}} = \frac{f^2 \cdot N}{k \cdot d}$

Abhängigkeiten

Aus der Näherungsformel kann leicht abgelesen werden, dass die hyperfokale Entfernung d_h zunimmt und der Schärfentiefebereich somit abnimmt, wenn die Brennweite f zunimmt, die Blendenzahl k kleiner wird (respektive die Blendenöffnung größer) oder der Zerstreuungskreis Z kleiner sein darf.

Zusammenhang zwischen Bildwinkel α, Bildweite b und Bilddiagonale d

Die Abhängigkeit zwischen hyperfokaler Entfernung d_h und verwendeter Bilddiagonalen d kann mit folgender Überlegung leicht abgeschätzt werden: Die Brennweite f ist für unendlich große Gegenstandsweiten identisch mit der Bildweite b, so dass die Brennweite für große Gegenstandsweiten näherungsweise wie folgt von der Bilddiagonalen d abhängt:

$f \approx b = \frac{d}{2 \cdot tan (\frac{\alpha}{2})}$, wobei α der gewünschte Bildwinkel ist, der für die perspektivische Bildwirkung maßgeblich ist.

Setzt man diese Näherung in die Näherungsgleichung für die hyperfokale Entfernung ein, ergibt sich:

$d_h \approx \frac {d}{k} \cdot \frac{N}{4 \cdot tan^2 (\frac{\alpha}{2})}$

Dies bedeutet, dass die hyperfokale Entfernung d_h linear mit der Bilddiagonalen d zunimmt, wenn die Blendenzahl k, die Anzahl der Bildpunkte N auf der Bilddiagonalen und der Bildwinkel α konstant gehalten werden. Ebenso kann der Formel abgelesen werden, dass die Schärfentiefe umso geringer ist, je kleiner die Blendenzahl oder der Bildwinkel sind; Weitwinkelobjektive haben also bei sonst gleichen Voraussetzungen einen größeren Schärfentiefebereich als Teleobjektive, beziehungsweise die hyperfokale Entfernung ist bei Weitwinkelobjektiven kleiner als bei Teleobjektiven.

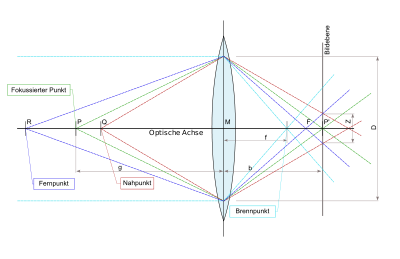
Nahpunkt

Anschließend können wir die Entfernung vom Linsenmittelpunkt zum Nahpunkt d_n berechnen:

$d_n = \frac{g \cdot d_h}{d_h + (g-f)}$

Für hinreichend große Gegenstandsweiten gegenüber der Brennweite kann die Brennweite in der Differenz der beiden Größen (g − f) vernachlässigt werden, und es ergibt sich:

$d_n \approx \frac{g \cdot d_h}{d_h + g} = \frac{d_h}{\frac {d_h}{g} + 1}$

Wird ferner die Gegenstandsweite g für ein abbildendes System auf die hyperfokale Entfernung d_h eingestellt, also mit der Bedingung $\frac{d_h}{g}=1$, dann liegt der Nahpunkt bei der halben hyperfokalen Entfernung, und in diesem Fall werden Gegenstände von unendlich bis zur halben hyperfokalen Entfernung scharf abgebildet (Faustregel):

$d_n \approx \frac{d_h}{2}$

Fernpunkt

Verschiedene Strahlengänge zur Bestimmung der Schärfentiefe. Fokussierung vor der hyperfokalen Entfernung. Der Fernpunkt liegt nicht im Unendlichen.

Ebenso können wir die Entfernung vom Linsenmittelpunkt zum Fernpunkt d_f berechnen:

$d_f = \begin{cases} \frac{g \cdot d_h}{d_h-(g-f)}, & \text{wenn } d_h > (g-f) \\ \infty, & \text{wenn } d_h \le (g-f) \end{cases}$

Für hinreichend große Gegenstandsweiten gegenüber der Brennweite kann auch hierbei die Brennweite in der Differenz der beiden Größen (g − f) vernachlässigt werden, und es ergibt sich entsprechend:

$d_f \approx \frac{g \cdot d_h}{d_h - g} = \frac{d_h}{\frac {d_h}{g} - 1}$

Schärfentiefebereich

Der Schärfentiefebereich Δ_d erstreckt sich vom Nahpunkt d_n bis zum Fernpunkt d_f mit

$\Delta_d = d_f-d_n = \begin{cases} 2 \frac{ g(g-f)d_h}{d_h^2-(g-f)^2}, & \text{wenn } d_h > (g-f) \\ \infty, & \text{wenn } d_h \le (g-f) \end{cases}$

beziehungsweise unter Vernachlässigung der Brennweite bei ${g \gg f}$:

$\Delta_d \approx \begin{cases} {{2 d_h} \over {({d_h \over g})^2 - 1}}, & \text{wenn } d_h > g \\ \infty, & \text{wenn } d_h \le g \end{cases}$

Wellenoptische Schärfentiefe

Alle optischen Abbildungen sind durch Beugung begrenzt, so dass ein einzelner Punkt niemals auf einen Punkt, sondern nur auf ein Beugungsscheibchen (oder Airyscheibchen) abgebildet werden kann. Die Trennschärfe zweier benachbarter Beugungsscheibchen definiert analog zum fotografischen Film einen maximal zulässigen Zerstreuungskreis. Nach dem Rayleigh-Kriterium muss die Intensität zwischen zwei benachbarten Bildpunkten um 20 Prozent abfallen, um als scharf zu gelten. Die Größe des Beugungsscheibchens ist abhängig von der Wellenlänge des Lichts. Man definiert die Rayleighsche Schärfentiefe als den Bereich, innerhalb dessen sich die Abbildungsgröße nicht ändert, das heißt konstant dem kleinstmöglichen (d.h. beugungsbegrenzten) Wert entspricht:

$d_R = \frac{\lambda}{2 \, n \sin^2 u}$

Hierbei ist λ die Wellenlänge, n die Brechzahl und u der Aperturwinkel des abbildenden Systems.

Die Rayleighsche Schärfentiefe ist bei beugungsbegrenzten optischen Systemen relevant, zum Beispiel in der Mikroskopie oder in der Fotolithografie. In der Fotografie macht sich eine wellenoptische Unschärfe jenseits der förderlichen Blende k_f bildwirksam bemerkbar.

$k_f = \frac {Z}{1{,}22 \, \lambda \, (m+1)}$

Hierbei ist Z der maximal zulässige Zerstreuungskreis, m der Abbildungsmaßstab und λ die Wellenlänge.

Für übliche Anwendungen (kleiner Abbildungsmaßstab) in der Kleinbild-Fotografie ergibt sich eine förderliche Blende von über f/32, so dass Beugung außer in der Makrofotografie kaum eine Rolle spielt.

Da die kleinen Sensoren moderner Kompakt-Digitalkameras aber sehr kleine zulässige Zerstreuungskreise erfordern, rückt k_f in den Bereich üblicher Blendenzahlen. Für einen 1/1,8″-Sensor liegt die förderliche Blende zum Beispiel bei zirka f/8, im Nahbereich noch darunter.

Lochkamera

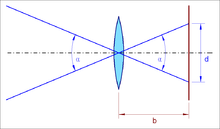
Bei einer Lochkamera hängt die Größe der Unschärfekreise von der Gegenstandsweite g, der Bildweite b und dem Lochdurchmesser D ab. Ein Objekt wird hinreichend scharf abgebildet, wenn gilt:

$D + \frac {D \cdot b} {g} \leqq Z$

Der Fernpunkt d_f einer Lochkamera liegt immer im Unendlichen. Für sehr große Gegenstandsweiten g vereinfacht sich die Bedingung zu: $D \leqq Z$. Das heißt, der Lochdurchmesser darf nicht größer werden als der zulässige Zerstreuungskreisdurchmesser, sonst ist mit einer Lochkamera auch im Fernbereich keine hinreichend scharfe Abbildung mehr möglich.

Anwendung in der Fotografie

Links: große Schärfentiefe mit Blende 8, rechts: mittlere Schärfentiefe mit Blende 2,8 (beides mit Kompaktkamera aufgenommen)
Durch den Einsatz einer kleineren Blende wird der Zerstreuungskreis verkleinert.
Das Freistellen eines Objektes durch geringe Schärfentiefe am Beispiel eines einzelnen Radfahrers, der aus dem Peloton herausgehoben wird.
Blende 22. Der scharf dargestellte Bereich reicht von vorne bis hinten.	Blende 10. Der scharf dargestellte Bereich liegt in der Mitte. Die Übergänge zu den unscharfen Bereichen sind deutlich sichtbar.	Blende 2. Der scharf dargestellte Bereich ist nun nur noch auf die Margeriten in der Bildmitte begrenzt. Nah- und Fernpunkt liegen nahe beieinander.

Manuelles Zoomobjektiv. Die Blendenkurven zeigen, wie die Schärfentiefe mit zunehmender Brennweite abnimmt.

Russische Soldaten

Bildgestaltung mit Schärfentiefe

Der gezielte Einsatz der Schärfentiefe durch Einstellen der Blende, der Entfernung und der Brennweite ermöglicht es, den Blick des Betrachters auf das Hauptmotiv zu lenken. Dazu schränkt der Fotograf die Schärfentiefe so eng wie möglich um die Ebene ein, auf der sich das Hauptmotiv befindet. Der Vorder- und Hintergrund wird dadurch unscharf abgebildet. Diese selektive Unschärfe lenkt weniger vom Hauptmotiv ab, das durch die selektive Schärfe akzentuiert wird.

Eine eingeschränkte Schärfentiefe kann bei fotografischen Aufnahmen mit punktförmigen Objekten, die sich etwas außerhalb der scharf abgebildeten Gegenstandsweite befinden, zu sogenannten Geisterflecken in der Aufnahme führen.

Bei kleinen Aufnahmeformaten, z. B. beim Erstellen von Ausschnittsvergrößerungen oder beim Einsatz von Digitalkameras mit kleinen Bildsensoren (Formatfaktor), verkleinert sich der maximal zulässige Zerstreuungskreis (bei gleichbleibender Pixelzahl), was den Schärfentiefebereich zunächst verkleinert. Die kleineren Aufnahmeformate erfordern jedoch proportional kleinere Objektivbrennweiten, um gleichbleibende Blickwinkel zu gewährleisten – das hingegen vergrößert den Schärfentiefebereich. Beides, die Verkleinerung der Bildsensoren (⇒ Verkleinerung der maximal zulässigen Zerstreuungskreise) und die deshalb notwendige Verkleinerung der Objektivbrennweiten, beeinflusst den Schärfentiefebereich. Die Einflüsse sind zwar gegensinnig, sie gleichen sich aber nicht aus. Der maximal zulässige Zerstreuungskreis geht linear und die Objektivbrennweite annähernd quadratisch in die Schärfentiefe ein – also überwiegt der Einfluss der Objektivbrennweite. Dadurch wird die Schärfentiefe entsprechend größer und es wird zunehmend schwieriger, die selektive Schärfe als fotografisches Gestaltungsmittel direkt beim Fotografieren einzusetzen. Damit sich beide Einflüsse ausgleichen, müsste die Pixeldichte der Sensoren annähernd quadratisch mit der Verkleinerung der Sensorabmessungen wachsen, was schnell an technische Grenzen führt.

Faktoren zur Beeinflussung der Schärfentiefe

Der Schärfebereich kann durch mehrere Faktoren (siehe Abschnitt Schärfentiefe berechnen) beeinflusst werden:

• Durch Abblenden der Blende wird er ausgedehnt und durch Aufblenden eingeengt. Je kleiner die Blendenöffnung ist, desto größer ist also der Schärfebereich.
• Eine weitere Einflussgröße auf die Schärfentiefe ist der Abbildungsmaßstab m. Der Abbildungsmaßstab hängt von der Brennweite des Objektivs f und der Gegenstandsweite g ab (b ist die Bildweite).

$m=\frac{b}{g} = \frac{f}{g-f}$

Je kleiner der Abbildungsmaßstab, desto größer ist die Schärfentiefe. Ein Weitwinkelobjektiv mit einer kürzeren Brennweite erzeugt, bei gleicher Gegenstandsweite, eine größere Schärfentiefe als ein Teleobjektiv mit einer langen Brennweite.

• Für Kamerasysteme mit unterschiedlichen Bilddiagonalen und somit entsprechend unterschiedlichen Normalbrennweiten gilt bei sonst gleichen Voraussetzungen (Blendenzahl, Bildwinkel und Bildauflösung), dass die Schärfentiefe umso geringer wird, je größer die Bilddiagonale ist. Es ist also mit größeren Kameras einfacher möglich, die Schärfentiefe einzuschränken (etwa bei Porträtaufnahmen mit unscharfem Hintergrund), als mit kleinen Kameras.
• Die Verteilung der Schärfentiefe vor und hinter dem fokussierten Objekt variiert mit der eingestellten Entfernung: Im engen Nahbereich wird ungefähr ein Verhältnis von 1:1 erreicht, mit wachsender Entfernung wächst der Anteil hinter dem fokussierten Objekt kontinuierlich an; letzteres extrem, wenn die Unendlicheinstellung noch eben in den Schärfebereich gelegt wird (= hyperfokale Entfernung).
• Die Schärfentiefe ändert sich in bestimmten Bereichen praktisch nicht, wenn ein Motiv einmal mit kurzer Brennweite aus geringer Entfernung und einmal mit langer Brennweite aus größerer Entfernung derart abgebildet wird, dass es im Bild die gleiche Größe hat. Der vorgenannte Einfluss der Brennweite wird durch die andere Gegenstandsweite kompensiert. Diese Regel gilt, wenn in beiden Fällen die gleiche Blende verwendet wird und wenn die Entfernung zum Motiv bei der kurzen Brennweite kleiner als etwa ein Viertel der hyperfokalen Entfernung ist.

Kameraeinstellungen

Im Makrobereich ist die Schärfentiefe s allein durch Abbildungsmaßstab, eingestellte Blende und erlaubtem Unschärfekreisdurchmesser definiert. Sie ist (solange der erlaubte Unschärfekreis deutlich kleiner als die Brennweite ist) vollständig unabhängig von der Brennweite.

Sie berechnet sich zu:

Verkleinerungsfaktor = 1 / Abbildungsmassstab

v = Verkleinerungsfaktor² + Verkleinerungsfaktor

$s = 2 \cdot \text{Unsch}\mathrm{\ddot a}\text{rfekreisdurchmesser}\cdot \text{Blendenzahl}\cdot v$

Im Nichtmakrobereich (der Fehler übersteigt 10 % ab: Verkleinerungsfaktor > 0,3·Brennweite/Unschaerfekreisradius/Blendenzahl) muss die Formel um den Korrekturwert 1 − w² erweitert werden zu:

v = Verkleinerungsfaktor² + Verkleinerungsfaktor

$w = \text{Unsch}\mathrm{\ddot a}\text{rfekreisradius}\cdot \text{Blendenzahl} \cdot \text{Verkleinerungsfaktor}/\text{Brennweite}$

$s = 2\cdot\text{Unsch}\mathrm{\ddot a}\text{rfekreisdurchmesser} \cdot \text{Blendenzahl}\cdot v/(1-w^2)$

Der Gültigkeitsbereich dieser Formel endet, wenn man negative Werte erhält. Dann liegt der Fernpunkt im Unendlichen, der Schärfentiefebereich ist dann unendlich groß, der Fernpunkt liegt hinter dem Objektiv, konkave Wellenfronten liegen innerhalb des Fokusbereichs.

Zur praktischen Anwendung im Feld:

• man merkt sich $2\cdot 10\cdot\text{Unsch}\mathrm{\ddot a}\text{rfekreisdurchmesser}$ für seine aktuelle Kamera (bei vielen Crop-DSLRs um die 0,4 mm)
• Für einen Verkleinerungsfaktor von 10, 5, 2, 1 muss man diesen Wert mit 110, 30, 5 bzw. 2 multiplizieren (und erhält 44 mm, 12 mm, 2 mm bzw. 0,8 mm).
• Das ergibt die Schärfentiefe für die Blendenzahl 10. Für andere Blendenzahlen erhöht bzw. verringert sich dieser Wert proportional.

Weitere Bemerkungen:

Tilt-Shift-Objektiv von Nikon

Scheimpflug-Einstellung in der Großformatkamera.

• Einige elektronisch gesteuerte Kameras bieten die Möglichkeit an, zuerst den vorderen und dann den hinteren Punkt des gewünschten Schärfebereiches mit dem Auslöser zu markieren (DEP-Funktion). Die Kamera berechnet dann die dafür benötigte Blende und stellt den Fokus so ein, dass die Schärfe genau dem markierten Bereich entspricht. Die A-DEP-Funktion aktueller Digitalkameras hat damit allerdings nichts zu tun, hier bestimmt die Kamera den vorderen und hinteren Schärfepunkt durch Nutzung aller AF-Felder.
• Die Verstellmöglichkeiten von Fachkameras erlauben das Nutzen der sogenannten Scheimpflug-Einstellung. Diese verändert nicht den Schärfenbereich des Objektivs, sondern erlaubt, die Schärfeebene zu verlagern und damit an das Motiv anzupassen. Für Klein- und Mittelformatkameras gibt es für den gleichen Einsatzzweck spezielle Tilt- bzw. Swing-Balgengeräte bzw. sogenannte Tilt-Objektive, eine Funktion, die oft auch mit einer Shift-Funktion zur möglichen Parallelverschiebung der Schärfenebene kombiniert wird.
• Einige Spezialobjektive verfügen über die Funktion der variablen Objektfeldwölbung (VFC, variable field curvature), die rotationssymmetrisch die stufenlose konvexe oder konkave Durchbiegung der Schärfenebene erlaubt.

Anwendungen in der Computergrafik

Viele bekannte Verfahren in der Computergrafik nutzen aus Gründen der Geschwindigkeit direkte Transformationen (z. B. über Matrixmultiplikationen), um die Geometrie in Bilddaten zu überführen. Durch diese mathematischen Konstrukte ergibt sich jedoch auch eine unendliche Schärfentiefe. Da die Schärfentiefe jedoch auch als gestalterisches Mittel eingesetzt wird, haben sich verschiedene Methoden durchgesetzt, um diesen Effekt nachzuahmen.

In 3D-Computerspielen hat sich das direkte Rendering von Polygonen durchgesetzt. Dieses Verfahren besitzt diverse Geschwindigkeitsvorteile gegenüber dem indirekten Rendering (Raytracing), hat aber auch zugleich bestimmte technische Einschränkungen. So lässt sich die Tiefenschärfe nicht direkt berechnen, sondern muss in einem Postprocessing-Schritt mit Hilfe eines geeigneten Filters approximiert werden. Es handelt sich dabei um selektive Weichzeichner, die den Z-Buffer zur Kantenerkennung nutzen. Dadurch wird verhindert, dass beim Weichzeichnen des Bildes weiter vorn stehende Objekte in die Filterung des Hintergrunds mit einbezogen werden und umgekehrt. Probleme treten dabei insbesondere bei transparenten Objekten auf, da diese in separaten Postprocessing-Schritten behandelt werden müssen, was sich negativ auf die Geschwindigkeit des Bildaufbaus auswirkt.

Beim indirekten Rendering kann sowohl die zuvor beschriebene Methode als auch Multisampling verwendet werden, wobei zur Erzeugung eines Tiefenschärfeneffekts sehr viele Samples nötig sind. Deshalb werden diese Verfahren vorzugsweise in Renderern eingesetzt, die unbiased sind. Diese entsprechen einem sehr nah an dem Modell einer Kamera angelehnten Verfahren, wo einzelne Photonen/Rays und deren Farbwert auf einem Film akkumuliert werden, d. h., mit fortlaufender Berechnung und höherer Samplezahl wird das Bildrauschen immer weiter reduziert. Im Gegensatz zu ersterem Verfahren erzeugt es glaubhaftere und realistischere Ergebnisse (Bokeh, etc.), ist jedoch auch um Größenordnungen langsamer, weshalb es sich (noch) nicht für Echtzeitgrafik eignet.

• 

  Rendering einer Lupe mit unendlicher Schärfentiefe

• 

  Dieselbe Grafik mit endlicher Schärfentiefe und Fokus auf den vergrößerten Text

Die Berechnung beider obiger Bilder erfolgte mit Hilfe eines Unbiased Renderers. Zur hinreichenden Rauschunterdrückung waren 2500 Samples pro Pixel notwendig, was einer Verfolgung von ca. 11,6 Milliarden Strahlengängen entspricht, die einschließlich multipler Spiegelungen und Brechungen in der Szene verfolgt wurden.

Bei bewegten Objekten wird aus dem gleichen Grund eine künstlich erzeugte Bewegungsunschärfe (engl. motion blur) eingerechnet.

Siehe auch

• 35-Millimeter-Adapter (Schärfentiefe für herkömmliche Videokameras)
• Deep focus cinematography (möglichst große Schärfentiefe im Film)
• Focus stacking (Erzeugung von Bildern mit außergewöhnlich großer Schärfentiefe)
• Bokeh (Erscheinungsbild im unscharfen Entfernungsbereich)

Einzelnachweise

1. ↑ Der Fotograf Emil Otto Hoppé gehörte zu den ersten, die das Manko sehr geringer Tiefenschärfen als ästhetisches Stilmittel verwendete. In seinem Selbstportrait von 1926 (Bild unten) sind nur ein kleiner Teil seiner Hand sowie die Augen scharf - Hoppé liebte Hände.
2. ↑ Schärfentiefe in der englischen Wikipedia: DOF
3. ↑ Beitrag des Sprachwissenschaftlers Anatol Stefanowitsch über die Konkurrenz der Bezeichnungen "Schärfentiefe" und "Tiefenschärfe" vom 4. April 2011. In diesem Beitrag wird die Möglichkeit erwogen, dass die beiden Begriffe eben nicht synonym für dasselbe Verwendung finden, sondern dass zwei unterschiedliche Dinge benannt werden sollen: nämlich zum einen die "Schärfentiefe" als Längeneinheit und zum anderen die "Tiefenschärfe" als photographischen Effekt, um einen Bereich des Hintergrundes (der "Raumtiefe") schärfer abzubilden.

Literatur

• Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. Verlag Harri Deutsch, Frankfurt/Main 1981, ISBN 3-87144-570-3, Kap. 6.4.3, S. 562–573
• Andreas Feininger: Andreas Feiningers Große Fotolehre. Neuauflage Heyne Verlag München 2001, ISBN 3-453-17975-7

Weblinks

 Commons: Depth of field – Album mit Bildern und/oder Videos und Audiodateien

• Schärfentiefe-, Abbildungsmaßstab- und Nahlinsenrechner (deutsch). Berücksichtigt u. a. auch Beugung und Vorsatzlinsen. Kann individuelle Schärfentiefe-Tabellen ausgeben. Für Digitalkameras etwas komplizierter zu handhaben.
• Schärfentiefenrechner in Java auf DOF-Rechner (deutsch und englisch).
• Vergleich verschiedener Blendenzahlen und deren Schärfentiefe in Bildern
• dofmaster Berechnen der Schärfentiefe für unterschiedliche Kameras und Brennweiten in Abhängigkeit von der Blende (englisch)