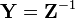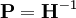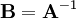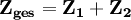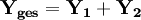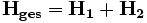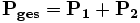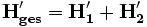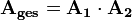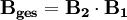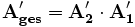Vierpoldarstellung

Eingangs- und Ausgangswiderstand eines Zweitores

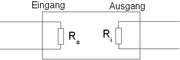
Ein Vierpol beschreibt in der Elektrotechnik ein Bauelement mit vier Anschlüssen (Klemmen) bzw. zwei Klemm-Paaren (Toren). Die Bezeichnung Vierpol stammt aus dem Jahr 1921 von Franz Breisig. Obwohl der Begriff weiter gefasst ist als der des Zweitores, werden beide oft synonym zueinander gebraucht. Ein Vierpol ist genau genommen nur dann ein Zweitor, wenn die Beträge der Ströme, die in den Vierpol hinein fließen, paarweise gleich sind. Dieser Artikel bezieht sich auf den Begriff Zweitor. Weil jedoch der Begriff Vierpol viel weiter verbreitet ist, wird dieser im Folgenden benutzt. Oft bezeichnet man eines der Klemmenpaare des Vierpols als Eingang und das andere als Ausgang.

Das Klemmverhalten eines Vierpols wird durch seine Übertragungsfunktion oder seinen Frequenzgang beschrieben. Hieraus lassen sich Vierpolgleichungen gewinnen, aus denen Vierpolparameter abgelesen werden können.

Charakterisierung

Ein Vierpol lässt sich anhand seines Verhaltens und seiner inneren Struktur wie folgt charakterisieren:

• Hängen die Vierpolströme und -spannungen linear voneinander ab, so nennt man den Vierpol linear, sonst nichtlinear.
• Enthält ein Vierpol keine Quellen (ungesteuert oder gesteuert), so nennt man ihn passiv, sonst aktiv.
• Ändert sich das Verhalten eines Vierpols beim Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht, so nennt man ihn symmetrisch, sonst unsymmetrisch.
• Ändert sich das Verhältnis von Eingangsstrom und Ausgangsspannung bei kurzgeschlossenem Eingang beim Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht, so nennt man einen solchen Vierpol reziprok oder umkehrbar (Reziprozitätstheorem).
• Hat eine sich (durch Belastung) verändernde Ausgangsgröße keinen Einfluss auf eine Eingangsgröße, so ist der Vierpol rückwirkungsfrei.

Parameter-Darstellungen

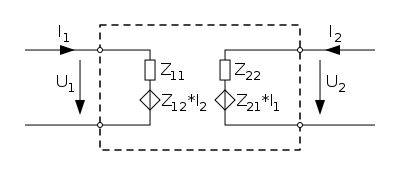
Bezeichnet U₁ die Spannung und I₁ den Strom am Eingangsklemmenpaar und U₂ und I₂ die entsprechenden Größen am Ausgangsklemmenpaar, so lassen sich unter der Voraussetzung der Existenz folgende Vierpolgleichungen aufschreiben. Eingeprägte Ströme und Spannungen werden je nach Bedarf zu diesen Gleichungen als Matrizen hinzuaddiert. Die angegebenen Berechnungsvorschriften dienen zur Bestimmung der Matrizen für einen beliebigen, bekannten Vierpol, wie zum Beispiel ein Feedback-Netzwerk einer Verstärkerschaltung.

Z-Charakteristik	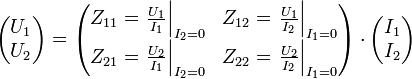	$\begin{pmatrix}U_1 \\ U_2\end{pmatrix} = \begin{pmatrix}Z_{11} = \left.\frac{U_1}{I_1}\right|_{I_2=0} & Z_{12} = \left.\frac{U_1}{I_2}\right|_{I_1=0} \\ Z_{21} = \left.\frac{U_2}{I_1}\right|_{I_2=0} & Z_{22} = \left.\frac{U_2}{I_2}\right|_{I_1=0}\end{pmatrix} \cdot \begin{pmatrix}I_1 \\ I_2\end{pmatrix}$		Z: Impedanzmatrix, existent, falls die Torströme (I1 bzw. I2) unabhängig wählbar sind.
Y-Charakteristik	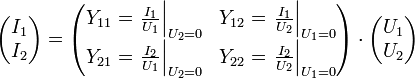	$\begin{pmatrix}I_1 \\ I_2\end{pmatrix} = \begin{pmatrix}Y_{11} = \left.\frac{I_1}{U_1}\right|_{U_2=0} & Y_{12} = \left.\frac{I_1}{U_2}\right|_{U_1=0} \\ Y_{21} = \left.\frac{I_2}{U_1}\right|_{U_2=0} & Y_{22} = \left.\frac{I_2}{U_2}\right|_{U_1=0} \end{pmatrix} \cdot \begin{pmatrix}U_1 \\ U_2\end{pmatrix}$		Y: Admittanzmatrix, existent, falls die Torspannungen (U1 bzw. U2) unabhängig wählbar sind.
H-Charakteristik	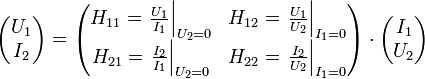	$\begin{pmatrix}U_1 \\ I_2\end{pmatrix} = \begin{pmatrix}H_{11} = \left.\frac{U_1}{I_1}\right|_{U_2=0} & H_{12} = \left.\frac{U_1}{U_2}\right|_{I_1=0} \\ H_{21} = \left.\frac{I_2}{I_1}\right|_{U_2=0} & H_{22} = \left.\frac{I_2}{U_2}\right|_{I_1=0} \end{pmatrix} \cdot \begin{pmatrix}I_1 \\ U_2\end{pmatrix}$		H: Hybridmatrix, existent falls I1 bzw. U2 unabhängig wählbar sind.
P-Charakteristik	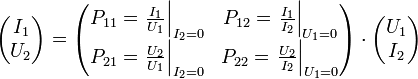	$\begin{pmatrix}I_1 \\ U_2\end{pmatrix} = \begin{pmatrix}P_{11} = \left.\frac{I_1}{U_1}\right|_{I_2=0} & P_{12} = \left.\frac{I_1}{I_2}\right|_{U_1=0} \\ P_{21} = \left.\frac{U_2}{U_1}\right|_{I_2=0} & P_{22} = \left.\frac{U_2}{I_2}\right|_{U_1=0} \end{pmatrix} \cdot \begin{pmatrix}U_1 \\ I_2\end{pmatrix}$		P: inverse Hybridmatrix, existent falls U1 bzw. I2 unabhängig wählbar sind.
A-Charakteristik	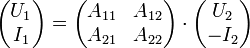	$\begin{pmatrix}U_1 \\ I_1\end{pmatrix} = \begin{pmatrix}A_{11} & A_{12}\\ A_{21} & A_{22}\end{pmatrix} \cdot \begin{pmatrix}U_2 \\ -I_2\end{pmatrix}$		A: Kettenmatrix
B-Charakteristik	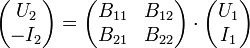	$\begin{pmatrix}U_2 \\ -I_2\end{pmatrix} = \begin{pmatrix}B_{11} & B_{12}\\ B_{21} & B_{22}\end{pmatrix} \cdot \begin{pmatrix}U_1 \\ I_1\end{pmatrix}$		B: inverse Kettenmatrix

Schaltung zur Impedanzmatrix

hierbei gilt im Fall der Existenz:

$\mathbf{Y}= \mathbf{Z}^{-1}$

$\mathbf{P}= \mathbf{H}^{-1}$

$\mathbf{B}= \mathbf{A}^{-1}$

Der Vorteil dieser Schreibweisen ist, dass die Parameter (Z_xy, etc.) bekannte Bauteilwerte repräsentieren und daher als Zahlenwerte gegeben sind. Nun kann der Zusammenhang zwischen den Eingangs- und Ausgangsströmen, sowie den Eingangs- und Ausgangsspannungen leicht abgelesen werden.

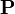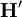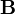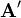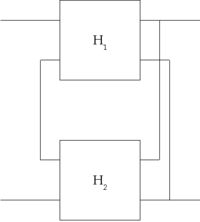
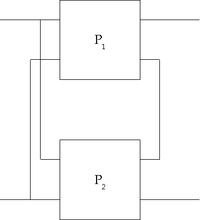
Hinweis: Statt dem Symbol $\mathbf{P}$ wird auch $\mathbf{H'}$ und statt dem Symbol $\mathbf{B}$ auch $\mathbf{A'}$ verwendet.

Zusammenschalten von Vierpolen

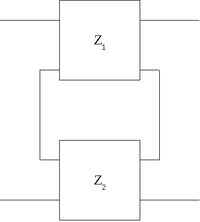
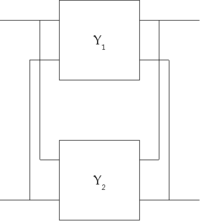
Zwei Vierpole können unter der Voraussetzung, dass die oben genannte Torbedingung an mindestens einem Tor erfüllt wird, zu einem neuen Vierpol zusammengeschaltet werden. Die Parameter des neu entstandenen Vierpols lassen sich aus den Parametern der beiden verschalteten Vierpole errechnen. Für jede Verschaltungsart gibt es eine Charakteristik, mit der sich die Verschaltung besonders gut berechnen lässt. Es gibt insgesamt 5 verschiedene Möglichkeiten, Vierpole zusammenzuschalten:

Beschreibungsart	Darstellung	Mathematische Beschreibung		Beschreibungsart	Darstellung	Mathematische Beschreibung
Reihenschaltung		$\mathbf{Z_{ges}}=\mathbf{Z_1}+\mathbf{Z_2}$		Parallelschaltung		$\mathbf{Y_{ges}}=\mathbf{Y_1}+\mathbf{Y_2}$
Hybridschaltung oder Reihen-Parallelschaltung		$\mathbf{H_{ges}}=\mathbf{H_1}+\mathbf{H_2}$		inverse Hybridschaltung oder Parallel-Reihenschaltung		$\mathbf{P_{ges}}=\mathbf{P_1}+\mathbf{P_2}$ bzw. $\mathbf{H'_{ges}}=\mathbf{H'_1}+\mathbf{H'_2}$
Kettenschaltung		$\mathbf{A_{ges}}=\mathbf{A_1}\cdot \mathbf{A_2}$ oder $\mathbf{B_{ges}}=\mathbf{B_2}\cdot \mathbf{B_1}$ bzw. $\mathbf{A'_{ges}}=\mathbf{A'_2}\cdot \mathbf{A'_1}$

Quellen

• Vorlesung Netzwerke 3 an der Technischen Universität Graz - Institut für Grundlagen und Theorie der Elektrotechnik
  Diese Thematik wird als Mehrtortheorie bezeichnet. Unter diesem Titel sollten daher weitere Quellen auffindbar sein.

• Vorlesung Dynamische Netzwerke an der Technischen Universität Dresden - Institut für Grundlagen der Elektrotechnik und Elektronik

Literatur

• Richard Feldtkeller: Einführung in die Vierpoltheorie der elektrischen Nachrichtentechnik. Hirzel, Stuttgart 1976 ISBN 3-7776-0319-8

Weblinks

• Passive Zweitore, Ronny Harbich, 2005

Siehe auch

• Zweipol
• Vierpolparameter
• Schaltungstheorie