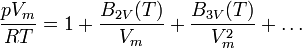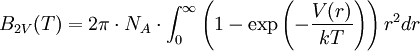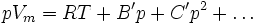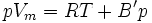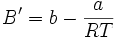Virialentwicklung

Virialgleichungen sind Erweiterungen der allgemeinen Gasgleichung durch eine Reihenentwicklung nach Potenzen von 1 / V_m. Sie stellen genäherte Zustandsgleichungen für reale Gase dar. Bei einem Abbruch der Reihenentwicklung nach dem ersten Glied erhält man wiederum die allgemeine Gasgleichung. Führt man die Reihenentwicklung jedoch weiter, entsteht eine potenziell unendliche Zahl von Zustandsgleichungen mit einer zunehmenden Anzahl von Parametern. In intensiver Form lautet die allgemeine Reihenentwicklung wie folgt:

$\frac{p V_m}{R T}=1 + \frac{B_{2V}(T)}{V_m} + \frac{B_{3V}(T)}{V_m^2} + \ldots$

Die einzelnen Formelzeichen stehen für folgende Größen:

• V_m - molares Volumen
• T - Temperatur
• p - Druck
• R - universelle Gaskonstante
• B_2V(T) - zweiter Virialkoeffizient
• B_3V(T) - dritter Virialkoeffizient (usw.)

Virialkoeffizienten

Die Virialkoeffizienten ergeben sich aus den Wechselwirkungen zwischen den Molekülen. Sie sind nicht physikalisch interpretierbar.

Der zweite Virialkoeffizient ergibt sich näherungsweise aus dem Paarpotential V(r) zwischen den Molekülen:

$B_{2V}(T) = 2 \pi \cdot N_A \cdot \int^\infty_0 \left( 1 - \exp \left( -\frac{V(r)}{k T} \right) \right) r^2 dr$

• N_A - Avogadro-Konstante
• k - Boltzmann-Konstante
• V - Paarpotential
• r - Abstand zwischen den Molekülen

Der dritte Virialkoeffizient hängt von den Wechselwirkungen innerhalb von Gruppen aus drei Molekülen ab, für alle weiteren gilt entsprechendes. Die Virialgleichung mit zwei oder drei Virialkoeffizienten ist nur im Bereich mäßiger Drücke gültig.

Verbindung zur Van-der-Waals-Gleichung

Eine andere, weiter verbreitete Zustandsgleichung für reale Gase, stellt die Van-der-Waals-Gleichung dar. Über eine Vereinfachung kann man zwischen dieser und der Virialgleichung mit zwei Virialkoeffizienten eine Verbindung herstellen.

$p V_m=R T + B' p + C' p^2 + \ldots \!$

Wird die Reihenentwicklung nach B' abgebrochen, berechnet sich dieser Korrekturfaktor nach dem Korrespondenzprinzip aus dem kritischen Zustand des jeweiligen Stoffes. Gleichzeitig ist diese Form der Virialgleichung auch eine vereinfachte Form der Redlich-Kwong-Gleichung.

$p V_m =R T+B' p \!$

$B'=b-\frac{a}{R T}$

Für die Parameter a und b siehe Van-der-Waals-Gleichung. Ist T gleich der Boyle-Temperatur, so gilt B' = 0.