Vollstetiger Operator

Ein kompakter Operator zwischen zwei Banachräumen ist in der Funktionalanalysis, einem der Teilgebiete der Mathematik, eine Abbildung mit einem „sehr dünnen“ Bild.

Definition

Seien E,F Banachräume, 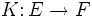$K\colon E\to F$ ein Operator. Dann heißt K kompakt, falls K stetig ist und das Bild jeder beschränkten Menge S in E eine relativkompakte Teilmenge von F ist.

Beispiel

Die Identität auf einem Banachraum ist genau dann kompakt, wenn der Banachraum endlich-dimensional ist. Dies folgt aus der Tatsache, dass die Einheitskugel genau dann relativkompakt ist, wenn der Banachraum endlich-dimensional ist.

Lineare kompakte Operatoren

Für lineare Operatoren reicht es zu fordern, dass das Bild der Einheitskugel 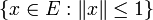$\{x \in E: \|x\| \le 1\}$ relativkompakt ist. Es ergibt sich dann folgender Zusammenhang zu stetigen Operatoren: Ist K stetiger linearer Operator, so wird jede beschränkten Menge auf eine beschränkte Menge abgebildet. Ist K kompakter linearer Operator, wird jede beschränkten Menge auf eine relativkompakte Menge abgebildet. Da jede relativkompakte Menge beschränkt ist, muss die Stetigkeit von K dann nicht mehr gefordert werden.

Vollstetige Operatoren

Seien E,F Banachräume, 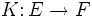$K\colon E\to F$ ein Operator. Dann heißt K vollstetig, falls für jede in E schwach konvergente Folge (x_n) die Bildfolge (K(x_n)) in F normkonvergent ist. Kompakte Operatoren sind vollstetig. Ist E reflexiv, so ist auch jeder vollstetige Operator kompakt. ^[1]

Eigenschaften

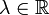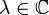• Für einen kompakten Operator K und einen Skalar $\lambda\in\R$ (bzw. $\lambda\in\mathbb{C}$) ist auch der Operator λK kompakt.
• Für kompakte Operatoren K₁ und K₂ ist auch der Operator K₁ + K₂ kompakt.
• Ist 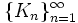$\{K_n\}_{n=1}^{\infty}$ eine Folge kompakter Operatoren die bezüglich der Operatornorm konvergiert, so ist auch 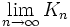$\lim_{n\to\infty}K_n$ kompakt.
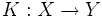• $K: X\to Y$ ist genau dann kompakt, wenn der adjungierte Operator 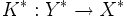$K^*: Y^*\to X^*$ kompakt ist.
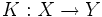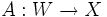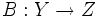• Seien W, X, Y und Z Banachräume, $K:X\rightarrow Y$ ein kompakter Operator, $A:W\rightarrow X$ und $B:Y\rightarrow Z$ beschränkte Operatoren. Dann ist auch 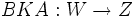$BKA:W\rightarrow Z$ kompakt.
• Insbesondere ist die Menge aller kompakten Operatoren eines Hilbertraumes H ein selbstadjungiertes abgeschlossenens Ideal in der C*-Algebra aller beschränkten linearen Operatoren auf H.
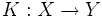• $K: X\to Y$ ist genau dann kompakt, wenn zu jeder beschränkten Folge (x_n) in X eine Teilfolge von (K(x_n)) existiert, welche in Y konvergiert. Kompakte Operatoren bilden also beschränkte Folgen auf Folgen mit konvergenten Teilfolgen ab. Ist X unendlichdimensional, gibt es beschränkte Folgen, die keine konvergenten Teilfolgen besitzen. Somit können kompakte Operatoren Konvergenzeigenschaften "verbessern".
• Ist 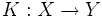$K: X\to Y$ ein linearer Operator und X endlichdimensional, so ist K kompakt

Eine wichtige Eigenschaft kompakter Operatoren ist, dass sie in folgendem Sinne "fast endlichdimensional" sind:

Gibt es eine Folge von Operatoren endlichen Ranges, welche in der Operatornorm gegen K konvergiert, so ist K kompakt.

In Hilberträumen gilt auch die Umkehrung, im Allgemeinen nicht.

Einzelnachweise

1. ↑ John B. Conway: A Course in Functional Analysis. 2. Auflage. Springer, ISBN 0-387-97245-5, VI, §3