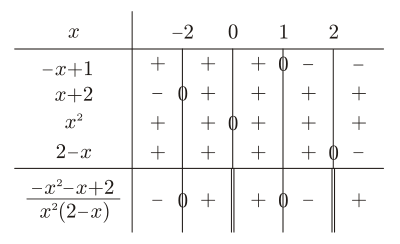Vorzeichentabelle

Eine Vorzeichentabelle ist in der Mathematik eine Methode, eine Ungleichung zu lösen oder die Vorzeichen einer Funktion zu ermitteln und tabellarisch darzustellen.

Anwendung

Die Vorzeichentabelle beruht auf der Tatsache, dass das Vorzeichen eines Produkts oder eines Quotienten sich aus den einzelnen Faktoren bestimmen lässt: die Multiplikation oder Division zweier Faktoren mit gleichem Vorzeichen ergibt einen positiven Term; bei unterschiedlichen Vorzeichen ergibt sich ein negativer Term. Eine Ungleichung kann gelöst werden, indem die der entsprechenden Gleichung zugrundeliegende Funktion ausgewertet wird.

In Frankreich ist die Verwendung der Vorzeichentabelle (franz. tableau de signes) fester Bestandteil des gymnasialen Mathematikprogramms.^[1]

In der Vorzeichentabelle werden Zeile für Zeile die einzelnen Faktoren der auszuwertenden Funktion dargestellt. In jeder Zeile wird deren Vorzeichen in Abhängigkeit von den Werten der Variable dargestellt, wobei Nullstellen durch einen durchgezogenen vertikalen Strich gekennzeichnet werden. Werte außerhalb des Definitionsbereichs werden durch einen vertikalen Doppelstrich markiert.

Weiterhin ist es üblich, nach Auswertung des Vorzeichens der Ableitung den Verlauf einer Funktion (monoton steigend oder fallend) sowie die lokalen Extremwerte in der Vorzeichentabelle grafisch darzustellen.

Beispiel

Zu lösen sei die Ungleichung $\frac{1}{x^2} \le \frac{1}{2-x}$, die für $x \in \mathbb{R} \backslash \{ 0, 2 \}$ definiert ist.

Diese Ungleichung lässt sich wie folgt schrittweise umformen:

$\begin{align} & \frac{1}{x^2}-\frac{1}{2-x} \le 0\\ \Leftrightarrow \quad & \frac{-x^2-x+2}{x^2(2-x)} \le 0\\ \Leftrightarrow \quad & \frac{(-x+1)(x+2)}{x^2(2-x)} \le 0 \end{align}$

Indem die vier Faktoren in einer Vorzeichentabelle eingetragen werden, kann das Vorzeichen der linken Seite der Ungleichung ermittelt werden:

Die Lösungsmenge der Ungleichung ist damit $L = ]{-\infty}, -2] \cup [1, 2[$.

Literatur

• Hoffmann Di Marzio u. a.: Mathematik für Fachoberschulen, Fachschulen – technische Fachrichtung, S. 64 ff. Bildungsverlag Eins, Troisdorf 2007, ISBN 3-427-21521-0

Weblinks

• Comprendre les maths, cours de seconde: Tableaux de signes (franz.)

Einzelnachweis

1. ↑ Bulletin Officiel du ministère de l’Education Nationale et du ministère de la Recherche 2001-156 du 7-8-2001 (PDF, 100 KB)