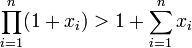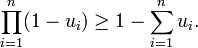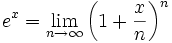- Weierstrass-Produkt-Ungleichung
-
In der Mathematik versteht man unter der bernoullischen Ungleichung eine einfache, aber wichtige Ungleichung, mit der sich eine Potenzfunktion nach unten abschätzen lässt.
Für jede reelle Zahl x
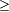 − 1 [1] und jede nicht negative ganze Zahl n
− 1 [1] und jede nicht negative ganze Zahl n 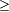 0 gilt
0 gilt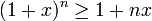 . [2]
. [2]
Benannt ist die Ungleichung nach dem schweizerischen Mathematiker Jakob Bernoulli.[3]
Inhaltsverzeichnis
Beweis
Die bernoullische Ungleichung lässt sich mit vollständiger Induktion beweisen.[4] Der Induktionsanfang n = 0 ist erfüllt:
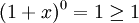 . [2]
. [2]
Als Induktionsvoraussetzung gelte nun
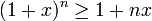 für
für 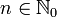 ,
, 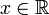 und
und 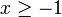 . Dann folgt wegen
. Dann folgt wegen 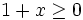 und der Induktionsvoraussetzung
und der InduktionsvoraussetzungNach dem Induktionsprinzip gilt die Behauptung für alle
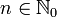 .
.Beispiel
Behauptung:
für alle reellen
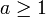 .
.Beweis: Zunächst sei
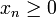 definiert durch
definiert durch![\sqrt[n]{a} = 1 + x_n](/pictures/dewiki/49/1340a42a4a2e9d6a774080ab108ff0d4.png) .
.
Dann gilt nach der Bernoulli-Ungleichung
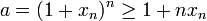 ,
,
also
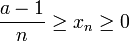 .
.
Es ist aber
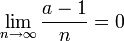 .
.
Damit ist dann auch
und letztlich
Verwandte Ungleichungen
Strikte Ungleichung
Ebenfalls als bernoullische Ungleichung wird folgende Ungleichung bezeichnet, die ein „strikt größer“ statt eines „größer gleich“ verwendet:
Für alle reellen Zahlen x > − 1, x
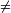 0 und alle natürlichen Zahlen n
0 und alle natürlichen Zahlen n 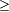 2 gilt
2 gilt- (1 + x)n > 1 + nx.
Der Beweis lässt sich ebenfalls mit Induktion nach dem gleichen Muster wie der Beweis für die Formulierung mit „größer gleich“ durchführen.[3]
Reelle Exponenten
Für reelle Exponenten lassen sich folgende Verallgemeinerungen durch Vergleich der Ableitungen zeigen: Für alle x > − 1 gilt
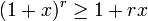 ,
,
wenn
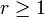 , und
, und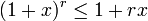 ,
,
wenn
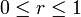 .
.Variable Faktoren
Betrachtet man keine Potenz, sondern ein Produkt unterschiedlicher Faktoren, so lässt sich folgende Verallgemeinerung mittels vollständiger Induktion zeigen:
falls
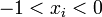 für alle
für alle 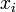 oder falls
oder falls 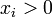 für alle
für alle 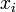 und n
und n 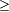 2.[3]
2.[3]Setzt man dabei
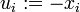 und betrachtet den Spezialfall
und betrachtet den Spezialfall 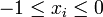 , also
, also 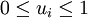 , so erhält man die sogenannte Weierstraß-Produkt-Ungleichung [5],[6],[7]
, so erhält man die sogenannte Weierstraß-Produkt-Ungleichung [5],[6],[7]Anwendungen
Exponentialfunktion
Trotz oder gerade wegen ihrer Einfachheit ist die bernoullische Ungleichung bei vielen Abschätzungen hilfreich. Fixiere ein festes
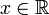 . Dann ist
. Dann ist 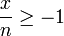 für alle
für alle 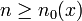 . Mit der bernoullischen Ungleichung gilt daher
. Mit der bernoullischen Ungleichung gilt daher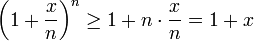 für alle
für alle 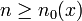 .
.
Wegen
ist somit die Ungleichung
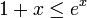 für alle
für alle 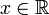
bewiesen.
Ungleichung vom arithmetischen und geometrischen Mittel
→ Hauptartikel: Ungleichung vom arithmetischen und geometrischen Mittel - Beweis aus Bernoulli-Ungleichung
Unter Verwendung einer Abschätzung mit der bernoullischen Ungleichung lässt sich die Ungleichung vom arithmetischen und geometrischen Mittel induktiv beweisen.
Quellen und Bemerkungen
- ↑ In der Tat gilt die Ungleichung sogar für x
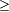 − 2 und ungerade n
− 2 und ungerade n 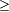 3, allerdings lässt sich dies nicht mehr mit vollständiger Induktion, sondern nur durch Vergleich der Ableitungen zeigen. Dazu zeigt man, dass f(x): = (1 + x)n − (1 + nx) für − 2 < x < − 1 negative Ableitung und damit keine Extrema hat, während der Wert für x = − 2 und x = − 1 positiv ist. In diesem Fall hat f ein lokales Maximum in x = − 2.
3, allerdings lässt sich dies nicht mehr mit vollständiger Induktion, sondern nur durch Vergleich der Ableitungen zeigen. Dazu zeigt man, dass f(x): = (1 + x)n − (1 + nx) für − 2 < x < − 1 negative Ableitung und damit keine Extrema hat, während der Wert für x = − 2 und x = − 1 positiv ist. In diesem Fall hat f ein lokales Maximum in x = − 2. - ↑ a b Für den Fall x = − 1 und n = 0 muss 00 = 1 vereinbart werden.
- ↑ a b c Harro Heuser, Lehrbuch der Analysis, Teil 1., B. G. Teubner Stuttgart, 1984, ISBN 3-519-22221-3, S. 61, Kapitel 7.9 und S. 68, Aufgabe 7.17
- ↑ http://mo.mathematik.uni-stuttgart.de/inhalt/erlaeuterung/erlaeuterung39/
- ↑ http://planetmath.org/encyclopedia/WeierstrassProductInequality.html
- ↑ http://mathworld.wolfram.com/WeierstrassProductInequality.html
- ↑ http://www.cut-the-knot.org/Generalization/wineq.shtml
Wikimedia Foundation.

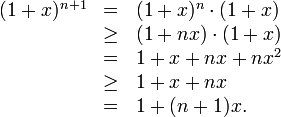
![\lim_{n \to \infty}\sqrt[n]{a} = 1](/pictures/dewiki/49/16026c088fbbca47d7fbe73413059ea3.png)
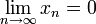
![\lim_{n \to \infty}\sqrt[n]{a} = 1 + \lim_{n\to\infty}x_n = 1 + 0 = 1.](/pictures/dewiki/102/f1b8076249eb07cf0c9bcf520e5174ba.png)