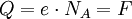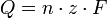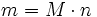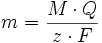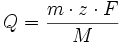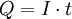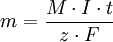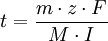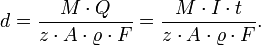Zweites Faradaysches Gesetz

Die nach ihrem Entdecker Michael Faraday benannten Faradayschen Gesetze beschreiben den Zusammenhang zwischen Ladung und Stoffumsatz bei der Elektrolyse. Sie sind daher die Grundgesetze der Elektrolyse.

Grundbegriffe der Elektrolyse

Die Elektrolyse, eine Methode der Elektrochemie, erlaubte es im 19. Jahrhundert erstmals einige neue Metalle in elementarer Form darzustellen. Dabei wird ein elektrischer Strom durch eine Schmelze aus Verbindungen dieser Metalle geleitet. Diese Methode nannte Faraday Elektrolyse (nach einem griechischen Ausdruck für „mittels Elektrizität befreien“).

Faraday bezeichnete eine Flüssigkeit oder eine Lösung, die elektrische Leitfähigkeit besaß, als Elektrolyt. Die Metallstäbe, die in die Flüssigkeit oder Lösung eingetaucht wurden, bezeichnete er als Elektroden (nach dem griechischen Wort für „die Straße der Elektrizität“). Die positiv geladene Elektrode nannte er Anode (ἄνοδος „Aufstieg“), die negativ geladene Elektrode Kathode (κάϑοδος „Hinabweg“).

Faraday verglich den Elektrizitätsfluss mit Wasser, das von oben (bei Elektrizität also von der Anode) nach unten (zur Kathode) fließt. Er folgte damit dem Beispiel Franklins, der einen Elektrizitätsfluss von positiv nach negativ definiert hatte. Das ist auch die Transportrichtung von positiv geladenen Ladungsträgern.

Weil in metallischen Leitern negative Ladungsträger bewegt sind, glauben viele dass die Stromrichtung verkehrt definiert sei. Aber die Definition sagt nichts über das Vorzeichen der Ladung der Ladungsträger aus. In Elektrolyten befinden sich positive und negative Ladungsträger, die Ionen genannt werden, während in metallischen Leitern die Ladungsträger negativ geladene Elektronen sind. Positiv geladene Ionen werden Kationen und negative geladene Anionen genannt. Die Bezeichnung leitet sich aus dem Namen der Elektrode umgekehrten Vorzeichens ab, an der diese Ionen abgeschieden werden.

Faradays Gesetze

Im Jahre 1832 stellte Faraday die Grundgesetze der Elektrolyse, heute bekannt als Faradaysche Gesetze, auf:

1. Faradaysches Gesetz

Die Stoffmenge, die an einer Elektrode während der Elektrolyse abgeschieden wird, ist proportional zur Ladung, die durch den Elektrolyten geschickt wird.

2. Faradaysches Gesetz

Die durch eine bestimmte Ladung abgeschiedene Masse eines Elements ist proportional zur Atommasse des abgeschiedenen Elements und umgekehrt proportional zu seiner Wertigkeit, daher zur Anzahl von einwertigen Atomen, die sich mit diesem Element verbinden können.

Heutige Formulierung

Um ein Mol eines einwertigen Ions elektrolytisch abzuscheiden, braucht es die Ladungsmenge bzw. Ladung Q:

$Q = e \cdot N_A = F$

Dabei ist e die Elementarladung und N_A ist die Avogadro-Konstante, die besagt, wie viele Teilchen ein Mol enthält. F ist die Faraday-Konstante und sie ist gleich der Ladung, die zur Abscheidung eines Mols eines einwertigen Stoffes benötigt wird. Sie ist auch gleich dem Betrag der Ladung eines Mols Elektronen, der zur Abscheidung benötigt bzw. abgegeben wird.

Um eine beliebige Stoffmenge eines z-wertigen Ions elektrolytisch abzuscheiden braucht es die Ladung:

$Q = n \cdot z \cdot F$

mit der Ladungszahl z des verwendeten Ions, der Stoffmenge n und der Faraday-Konstante F.

Wegen der Definition der molaren Masse M kann für die Masse m eines Stoffes geschrieben werden:

$m = M \cdot n$

mit Masse m des Stoffes, der molaren Masse M und der Stoffmenge n des Stoffes. Wird nun die zweite Gleichung nach n umgestellt und in die Gleichung der Masse m eingesetzt, so folgt:

$m = {M \cdot Q \over z \cdot F}$

Dabei ist hier die Masse m die Masse des durch Elektrolyse abgeschiedenen Stoffes. Durch Umstellen dieser Gleichung erhält man die Ladung Q, die notwendig ist eine bestimmte Masse m des Stoffes durch Elektrolyse abzuscheiden:

$Q = {m \cdot z \cdot F \over M}$

Bei konstanter Stromstärke I ist die Ladung Q der Elektrolysezeit t proportional:

$Q = I \cdot t$

Wird dies in die Gleichung über die Masse m des elektrolytisch abgeschiedenen Stoffes eingesetzt, so folgt:

$m = {M \cdot I \cdot t \over z \cdot F}$

Diese Gleichung sagt aus, wie groß die abgeschiedene Masse m des Stoffes in Abhängigkeit von der (konstanten) Stromstärke und der Elektrolysezeit ist. Dabei sind M und F Konstanten. Durch Umstellen dieser Gleichung erhält man für die Elektrolysezeit t:

$t = {m \cdot z \cdot F \over M \cdot I}$

Diese Gleichung besagt, wie lange die Elektrolysezeit sein muss, um eine bestimmte Masse eines abgeschiedenen Stoffes bei einer gegebenen konstanten Stromstärke elektrolytisch abzuscheiden.

Anwendungen

Eine interessante Anwendung der Faradayschen Gesetze ist der Gebrauch als Stütze der Atomtheorie, also als starker Hinweis, dass es Atome und Ionen gibt: Wie aufgrund des Millikan-Versuchs bekannt ist, ist die elektrische Ladung gequantelt, d. h. es gibt eine kleinste elektrische Ladung, die Elementarladung. Da gemäß den Faradayschen Gesetzen die Stoffmenge proportional zur Ladung ist, folgt sofort, dass bei der Elektrolyse die Stoffe in kleinsten Portionen umgesetzt werden, eben den Atomen oder den Ionen, die eine Ladung tragen, die entweder der Elementarladung oder einem vielfachen davon entspricht.

Weitere historisch wichtige Anwendungen sind die Bestimmung relativer Molmassen M und von Ladungszahlen z. Dazu wurden zum Beispiel zwei hintereinander geschaltete Elektrolysezellen benutzt, wobei etwa in der einen zwei Silberelektroden in eine Silbersalzlösung tauchen. Da die Zellen in Reihe geschaltet sind, fließt durch beide Zellen dieselbe Ladung, und wenn in der einen ein Mol Silber umgesetzt wird, wird in der anderen 1 mol/z umgesetzt.

Selbstverständlich werden die Faradayschen Gesetze auch in der Galvanik angewandt, wo sie z. B. bei bekannter geometrischer Oberfläche A eines Werkstücks die Abschätzung der Schichtdicke d erlauben. Nach der Definition der Dichte (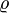$\varrho$) gilt

$\varrho = {m \over V} = {m \over d \cdot A}$.

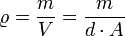Hierbei ist zu beachten, dass der Wirkungsgrad η der Galvanik bei 100% liegt und ggf. die Strommenge angepasst werden muss. Damit erhält man

$d = {M \cdot Q \over z \cdot A \cdot \varrho \cdot F} = {M \cdot I \cdot t \over z \cdot A \cdot \varrho \cdot F}.$