Millikan-Versuch

Beim Millikan-Versuch handelt es sich um ein Experiment, mit dem es dem amerikanischen Physiker Robert Andrews Millikan 1910 gelang, die Größe der Elementarladung e relativ präzise zu bestimmen.^[1][2] Für diese Leistung erhielt Millikan 1923 den Nobelpreis für Physik.

Millikan griff dazu auf zuvor von Harold Albert Wilson, Joseph John Thomson und anderen Forschern durchgeführte Versuche^[3] zurück, die er maßgeblich verbesserte. Millikans wichtigste Verbesserung bestand dabei darin, die zuvor eingesetzten Stoffe Wasser bzw. Alkohol durch schwerflüchtige Flüssigkeiten wie Öl und Quecksilber zu ersetzen.^[4]

Um die Elementarladung e zu bestimmen, maß Millikan in seinem Versuch die Steig- bzw. Sinkgeschwindigkeit von elektrisch aufgeladenen Öltröpfchen bei ein- und ausgeschaltetem elektrischem Feld. Er ermittelte einen Wert der Elementarladung von

$e = 4{,}774 \cdot 10^{-10}$ ESU $= 1{,}592 \cdot 10^{-19}$ Coulomb^[5].

Seit Millikans Zeiten ist sein Versuchsaufbau wiederholt durch präzisere Methoden der Elementarladungsbestimmung ersetzt worden, der genaueste Wert dieser physikalischen Naturkonstanten beträgt heute e = 1,602 176 565 (35) × 10⁻¹⁹ C.^[6]

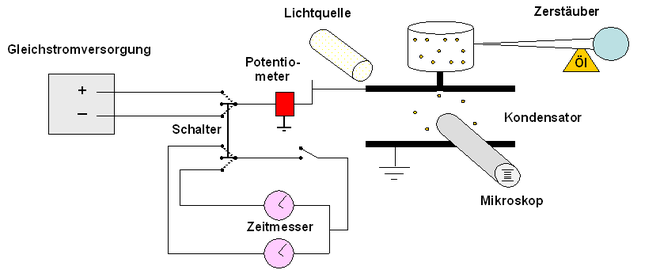
Versuchsaufbau und prinzipielle Vorgehensweise

Schematischer Versuchsaufbau des Millikan-Versuchs bei Verwendung der „Zweifeldmethode“

Elektrisch geladene Tröpfchen im Feld eines Plattenkondensators

Mit einem Zerstäuber werden zunächst feinste Öltröpfchen erzeugt, die allerdings so klein (etwa 0,5 µm) sind, dass man sie mit einem herkömmlichen Mikroskop nicht mehr direkt beobachten kann. Um sie dennoch zu verfolgen, bedient man sich der Dunkelfeldmethode, bei der man die Öltröpfchen in einem Winkel von etwa 150° zum Betrachter, also aus fast entgegengesetzter Richtung beleuchtet und die dabei entstehenden Beugungsscheibchen im Mikroskop verfolgt (wobei zu beachten ist, dass das Mikroskop oben und unten vertauscht, man also die Beugungsscheibchen sinkender Öltröpfchen nach oben wandern sieht und umgekehrt). Wenigstens ein Teil der Öltröpfchen muss dabei elektrisch geladen sein, was in Millikans Versuchsaufbau durch eine Röntgenröhre erreicht wurde, deren ionisierende Strahlung die Öltröpfchen elektrostatisch auflud. In der Regel aber genügt schon die Reibung der Öltröpfchen aneinander beim Zerstäuben oder an der Luft, um sie hinreichend aufzuladen. Anschließend gelangen die Tröpfchen in das Innere eines Plattenkondensators, in dem zunächst einmal alle Tröpfchen zwei Kräften ausgesetzt sind: zum einen der die Tröpfchen nach unten ziehenden Gravitationskraft, zum anderen der dem archimedischen Prinzip zufolge wirkenden Auftriebskraft der Tröpfchen in der Luft, die sie nach oben zieht. Schaltet man schließlich das elektrische Feld des Kondensators ein, kommt als dritte, nur auf die geladenen Öltröpfchen wirkende Kraft die Coulomb-Kraft des elektrischen Feldes hinzu, die die Tröpfchen je nach Polung des Kondensators nach oben oder unten zieht.

Der nicht erreichbare Schwebefall

Montiert man die Platten des Kondensators horizontal übereinander, kann man durch Anlegen einer geeigneten Spannung an die Platten eine elektrische Kraft auf die Tröpfchen ausüben, die die Summe der beiden erstgenannten Kräfte kompensiert, die nach unten wirkenden Gewichtskraft F_G sich also die Waage mit der Summe der elektrischen Kraft F_E sowie der Auftriebskraft F_A hält und das betreffende Öltröpfchen damit im Prinzip schwebt.

Durch Lösen der Gleichung F_E = F_G − F_A könnte nun also vom Grundsatz her die Ladung der Öltröpfchen bestimmt werden - praktisch aber scheitert das daran, dass die Beugungsscheibchen im Mikroskop keinerlei Rückschlüsse auf den Radius der Öltröpfchen zulassen, die rechte Seite der Gleichung also unbestimmt bleibt. Hinzu kommt, dass der Schwebezustand aufgrund der brownschen Bewegung nur schwer exakt zu erkennen ist.

Indirekte Bestimmung des Tröpfchenradius über die stokessche Reibung

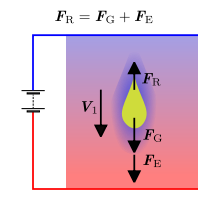
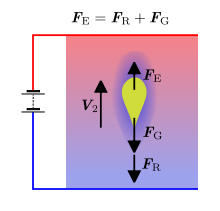
Um den Radius der Tröpfchen dennoch zu ermitteln, kann man den Umstand nutzen, dass sich nicht nur durch das elektrische Feld im Kondensator, sondern auch durch den Einfluss der geschwindigkeitsabhängigen stokesschen Reibungskraft ein Kräftegleichgewicht einstellt, allerdings nun nicht in Form eines Schwebezustands der betreffenden Öltröpfchen, sondern einer konstanten Geschwindigkeit v ihres Fallens bzw. Steigens.

In der Praxis gibt es dazu zwei verschiedene Verfahren: Bei der „Einfeldmethode“ misst man nach Erreichen des annäherndem Schwebezustands eines ausgewählten Öltröpfchens seine Fallgeschwindigkeit allein aufgrund der Schwerkraft, bei der „Zweifeldmethode“ dagegen lässt man das Öltröpfchen zunächst einmal vom Feld des Kondensators nach unten und (nach Umpolen des Feldes) anschließend wieder nach oben ziehen, wobei man jeweils die Sinkgeschwindigkeit v₁ sowie Steiggeschwindigkeit v₂ des Tröpfchens protokolliert.

Berechnungen

Die Schwebemethode (Einfeldmethode)

Ein ausgewähltes Öltröpfchen wird durch Variation der Kondensatorspannung annähernd zum Stillstand (Schweben) gebracht und anschließend bei ausgeschaltetem elektrischem Feld seine Fallgeschwindigkeit gemessen.

Wirksame Kräfte

Der Millikan-Versuch - Herleitung der Formel für die beobachtete Ladungsmenge

1. Gewichtskraft (eines kugelförmigen Öltröpfchens im homogenen Schwerefeld der Erde): $F_\mathrm{G} = m g = \frac{4}{3} \, \pi r^3 \rho_\mathrm{Oel} g$
2. Auftriebskraft (einer Kugel in Luft): $F_\mathrm{A} = \frac{4}{3} \, \pi r^3 \rho_\mathrm{Luft} g$
3. Coulomb-Kraft im elektrischen Feld: $F_\mathrm{E} = q E = \frac{qU}{d}$
4. Stokessche Reibungskraft (nur beim Fallen des Tröpfchens): $F_\mathrm{R} = 6\,\pi\eta r v$

Dabei bedeuten:

• $\,\pi$ = Kreiszahl
• $\,\rho_\mathrm{Oel}$ = Dichte des Öls
• $\,\rho_\mathrm{Luft}$ = Dichte der Luft
• $\,g$ = Schwerebeschleunigung
• $\,U$ = Spannung am Plattenkondensator
• $\,d$ = Plattenabstand des Plattenkondensators
• $\,\eta$ = Viskosität der Luft
• $\,v$ = Sinkgeschwindigkeit des Öltröpfchens

Bestimmung des Radius des fallenden Öltröpfchens

Sobald sich beim Fallen des Öltröpfchens ein Gleichgewicht zwischen stokesscher Reibungskraft F_R und "effektiver" Gewichtskraft F_G-F_A eingestellt hat, gilt: $\,F_\mathrm{R} = F_\mathrm{G} - F_\mathrm{A}$. Um die Rechnung zu vereinfachen, verwendet man als "effektive" Dichte des Öltröpfchens die Differenz seiner Dichte und der der Luft $\,\rho = \rho_\mathrm{Oel} - \rho_\mathrm{Luft}$:

$6 \pi \eta v r = \frac{4}{3} r^3 \pi \rho g$

$r = \sqrt{\frac{9 v \eta}{2 \rho g}} = 3 \cdot \sqrt{\frac{v \eta}{2 \rho g}}$

Bestimmung der Ladung des schwebenden Öltröpfchens

Im Schwebezustand gilt analog der obigen Formel die Gleichung: $\,F_\mathrm{E} = F_\mathrm{G} - F_\mathrm{A}$, bei der man praktischerweise wieder mit der „effektiven“ Dichte des Öltröpfchens rechnet:

$\frac{qU}{d} = \frac{4}{3} r^3 \pi \rho g$

$q = \frac{\rho V g}{E} = \frac{ \rho \frac{4}{3} \pi r^3 g d}{U}$

Setzt man in die zuletzt erhaltene Gleichung für q den experimentell bestimmten Radius r des Öltröpfchens ein, erhält man damit zu guter Letzt den Zahlenwert seiner Ladung:

$q = \frac{9 \pi d}{U} \sqrt{\frac{2 \eta^3 v^3}{\rho g}}$

Die Gleichfeldmethode (Zweifeldmethode)

Bei gegebener Kondensatorspannung wird für ein ausgewähltes sich zunächst nach unten bewegendes Öltröpfchen seine Sinkgeschwindigkeit $\,v_1$, dann, nach Umpolung des Feldes bei zahlenmäßig beibehaltener Kondensatorspannung, seine Steiggeschwindigkeit $\,v_2$ bestimmt.

Wirksame Kräfte

Sinken im Feld

Steigen im Feld

1. Gewichtskraft (eines kugelförmigen Öltröpfchens im homogen
   angenommenen Schwerefeld der Erde): $F_\mathrm{G} = m g = \frac{4}{3} \, \pi r^3 \rho_\mathrm{Oel} g$
2. Auftriebskraft (einer Kugel in Luft): $F_\mathrm{A} = \frac{4}{3} \, \pi r^3 \rho_\mathrm{Luft} g$
3. Coulomb-Kraft im elektrischen Feld: $F_\mathrm{E} = q E = \frac{qU}{d}$
4. Stokessche Reibungskraft: $F_\mathrm{R} = 6\,\pi\eta r v$

Dabei bedeuten:

• $\,\pi$ = Kreiszahl
• $\,\rho_\mathrm{Oel}$ = Dichte des Öls
• $\,\rho_\mathrm{Luft}$ = Dichte der Luft
• $\,g$ = Schwerebeschleunigung
• $\,U$ = Spannung am Plattenkondensator
• $\,d$ = Plattenabstand des Plattenkondensators
• $\,\eta$ = Viskosität der Luft
• $\,v$ = Sink- bzw Steiggeschwindigkeit des Öltröpfchens

Berechnung von Tröpfchenradius und -ladung

Zur Vereinfachung der Rechnung wird auch im folgenden wieder nur mit der „effektiven“ Dichte der Öltröpfchen gerechnet, also der Differenz ihrer Dichte und der der Luft $\,\rho = \rho_\mathrm{Oel} - \rho_\mathrm{Luft}$:

$r = \sqrt{\frac{9 \eta (v_1 - v_2)}{4 \rho g}} = \frac{3}{2} \sqrt{\frac{\eta}{\rho g} (v_1 - v_2)}$

$q = \frac{3 \pi \eta r (v_1 + v_2)}{E} = \frac{3 \pi \eta r (v_1 + v_2) d}{U}$

Soll schließlich die Ladung q mit nur einer einzigen Formel berechnet werden, ohne dazu vorher separat den Tröpfchenradius r zu bestimmen, ergibt sich diese Formel aus obigen beiden wie folgt:

$q = \frac {\frac{9 \pi \eta}{2} \sqrt{\frac{\eta (v_1 - v_2)}{\rho g}} (v_1 + v_2) d}{U} = \frac{9 \pi d}{2 U} \sqrt{\frac{\eta^3 (v_1 - v_2)}{\rho g}} (v_1 + v_2)$

Dabei bedeuten:

• $\,\pi$ = Kreiszahl
• $\,\rho$ = Dichte des Öls – Dichte der Luft
• $\,g$ = Schwerebeschleunigung
• $\,U$ = Spannung am Plattenkondensator
• $\,d$ = Plattenabstand des Plattenkondensators
• $\,\eta$ = Viskosität der Luft
• $\,v_1$ = Betrag der Sinkgeschwindigkeit des Öltröpfchens
• $\,v_2$ = Betrag der Steiggeschwindigkeit des Öltröpfchens

Bestimmung der Elementarladung

Da jedes Öltröpfchen aus einer größeren Anzahl von Atomen besteht und nicht nur eine, sondern auch mehrere Ladungen tragen kann, ist jede berechnete Ladung q eines Öltröpfchens ein ganzzahliges Vielfaches der Elementarladung. Zeichnet man die Ladungsverteilung vieler Versuche in ein Schaubild ein, ergibt sich keine kontinuierliche Verteilung. Es zeigt sich, dass nur Vielfache der Elementarladung $e = 1{,}602 \cdot 10^{-19}\,\mathrm{C}$ auftreten können.

Eine einzelne Elementarladung auf einem Teilchen lässt sich nur dann beobachten, wenn die Spannung hoch genug ist, um gerade noch sichtbare Öltröpfchen mit einer Elementarladung mindestens im Schwebezustand zu halten. Das ist in den meisten Versuchsaufbauten nicht der Fall.

Weblinks

 Commons: Millikan-Versuch – Sammlung von Bildern, Videos und Audiodateien

• On the Elementary Electrical Charge and the Avogadro Constant (engl.) - Informationen zu Robert Millikan inklusive der Original-Publikation, erschienen 1913 im Physical Review ^[5]
• Remotely Controlled Lab (RCL) (Realexperiment, über das Internet fernbedienbar, siehe dort unter "RCLs")
• Millikan-Versuch auf der Website der Universität des Saarlandes (PDF-Datei; 116 kB)
• Öltröpfchenversuch von Millikan auf www.leifiphysik.de
• Materialien zum Millikan-Versuch zusammengestellt von T. Unkelbach
• Beschreibung des Millikan-Versuchs bei Lern-Online.net (PDF-Datei; 250 kB)
• Beschreibung des Millikan-Versuchs mit genauer Beschreibung der Optik (PDF-Datei, 158 kB, engl.)

Quellen

1. ↑ Millikan, R. A. (1911): The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes's Law in: Physical Review (Series 1) Vol. 32, S. 349 - 397, Issue 4 – April 1911 doi:10.1103/PhysRevSeriesI.32.349, eingereicht im Nov. 1910
2. ↑ Robert Millikan im Britannica Online
3. ↑ Phys. Rev. 1911, Seite 349
4. ↑ Phys. Rev. 1911, Seite 351, Anfang Kapitel 2
5. ↑ ^{a b} Millikan, R. A. (1913): On the Elementary Electrical Charge and the Avogadro Constant in: Physical Review (Series 2), Volume 2 109 - 143, Issue 2 – August 1913 (DOI: 10.1103/PhysRev.2.109)
6. ↑ CODATA Recommended Values. National Institute of Standards and Technology, abgerufen am 21. Juni 2011.  Die eingeklammerten Ziffern geben die geschätzte Standardabweichung für den Mittelwert an, der den beiden letzten Ziffern vor der Klammer entspricht.