⊤

Eine Tautologie (altgr. τὸ αὐτό tò autó „dasselbe“ und -logie) im Sinne der Logik ist eine Aussageform^[1], die unabhängig von den Wahrheitswerten ihrer Bestandteile stets wahr ist. Der Wahrheitswert einer Tautologie ist wie der der Kontradiktion allein eine Funktion der durch semantische Regeln definierten Wahrheitsbedingungen der in ihr enthaltenen logischen Konstanten.

Begriffe

Es gibt Tautologien der Aussagenlogik, der Prädikatenlogik, der Modallogik usw.

In einem engeren Sinn ist Tautologie nur die aussagenlogische Tautologie. In der zweiwertigen, klassischen Logik ist die Tautologie eine Aussage, die unabhängig davon, welche Wahrheitswerte man den in ihr vorkommenden atomaren Aussagen oder Aussagevariablen zuordnet, immer wahr ist.(Beispiele siehe unten.)

Synonyme für den Ausdruck „Tautologie“ sind: Verum (lat. verum „wahr“); Allgemeingültigkeit, (logische) Identität, allgemeingültige Aussage, gültiger Satz, logisch wahre Aussage, stets wahre Formel, (aussagen)logisches Gesetz. Tautologisch heißt allgemeingültig, logisch wahr.

In formaler Schreibweise drückt man die Tatsache, dass eine Aussage $\varphi$ eine Tautologie ist, folgendermaßen aus: $\models\varphi$

Symbol für die Tautologie ist das „T“.^[2]

Die kürzeste disjunktive Normalform aller Tautologien ist a v ¬ a (Reichenbach).

In der Sprechweise der Kripke-Semantik der Modallogik ist eine Tautologie eine Aussage, die in jeder möglichen Welt wahr ist.

In der formalen Semantik ist eine Formel genau dann eine Tautologie, „wenn sie in jedem Modell wahr ist“.^[3]

Interpretation und Wichtigkeit von Tautologien

Es ist eine "... Tatsache, dass alle Tautologien... (dasselbe) bedeuten; sie bedeuten nämlich nichts." Dieser Fall der „Leerheit“ ist aber kein „Fall der Sinnlosigkeit“. „Nicht von Bedeutung sein ist nicht dasselbe wie keine Bedeutung haben.“^[4] Wittgenstein: „Die Sätze der Logik sagen also nichts.“^[5]

Sprachpolitisch wird die Verwendung des Ausdrucks „Tautologie“ bei Wittgenstein und die Annahme, sie sei „sinnlos“, jedoch nicht „unsinnig“, als ein Ausdruck seiner nominalistischen Tendenz gesehen, die der von Frege diametral entgegengesetzt sei.^[6]

Dies ändert aber nichts daran, dass die Tautologie ein „zentraler Grundbegriff der modernen logischen Systeme“ ist^[7], den Bereich der logischen Formeln „konstituiert“^[8] und auch allgemein semantisch bereichernd sein kann.^[9]

Abgrenzungen

Tautologie - Kontradiktion - Kontingenz

Die Tautologie ist eine stets wahre, die Kontradiktion eine stets falsche und die Kontingenz eine wahre oder falsche Formel.

In der zweiwertigen Logik ist die Verneinung einer Kontradiktion eine Tautologie und die Verneinung einer Tautologie eine Kontradiktion.

Tautologie und analytisch wahre Sätze

In traditioneller philosophischer Terminologie sind Tautologien im logischen Sinn eine Unterklasse der analytisch wahren Sätze, die wahr sind nur aufgrund der in ihnen auftretenden Ausdrücke. Die Tautologie ist eine „leere Formel“, „leer im Sinne von analytisch“ (Reichenbach). Jede Tautologie ist ein analytisches Urteil, aber nicht umgekehrt.

Sie stehen damit im Gegensatz zu synthetischen Formeln.

Tautologie und Theorem (innerhalb eines Kalküls)

Das Konzept der Tautologie ist ein semantisches Konzept, also aus der Bedeutung einer Aussage definiert. Es muss klar unterschieden werden vom syntaktischen Konzept Theorem: Eine Aussage heißt Theorem, wenn sie innerhalb eines logischen Kalküls mittels der Axiome und Schlussregeln dieses Kalküls herleitbar ist.

Im Allgemeinen ist man beim Aufstellen eines Kalküls für logische Zwecke darum bemüht, ihn so zu formulieren, dass die in ihm ableitbaren Theoreme auch wirklich Tautologien sind. In diesem Fall spricht man von einem korrekten Kalkül. Ist ein Kalkül so konstruiert, dass sich in ihm alle Tautologien ableiten lassen, dann nennt man ihn vollständig. Für die klassische Aussagenlogik ist es möglich, Kalküle anzugeben, die sowohl korrekt als auch vollständig sind; bei mächtigeren logischen Systemen ist das aber nicht der Fall, wie der Gödelsche Unvollständigkeitssatz aussagt.

Tautologien in der zweiwertigen Aussagenlogik (Beispiele)

Einige Beispiele aus der klassischen, zweiwertigen Aussagenlogik:

Eine Tautologie ist zum Beispiel die Disjunktion „Es regnet, oder es regnet nicht“: Unabhängig davon, ob die in ihr vorkommende Aussage „Es regnet“ wahr ist oder nicht, ist die ganze Aussage wahr: Ist „Es regnet“ wahr, dann ist „Es regnet, oder es regnet nicht“ wahr, weil der erste Teilsatz der Disjunktion wahr ist. Ist „Es regnet“ aber falsch, dann ist damit „Es regnet nicht“ wahr. Dies wiederum ist aber der zweite Teilsatz der Disjunktion, sodass der ganze Satz auch in diesem Fall wahr ist.

Zur einfachen Verdeutlichung einer Tautologie gibt es auch eine amüsante Bauernregel: "Kräht der Hahn um 12 Uhr auf dem Mist, ändert sich das Wetter oder es bleibt wie es ist". Diese Aussage ist in jedem Fall richtig. Dies ist die Art, wie Tautologien strukturiert sind.

• Für jede Aussage A ist "Wenn A, dann A" eine Tautologie.

In Zeichen: $\models A \rightarrow A$

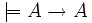
• Für jede Aussage A ist "A oder nicht A" eine Tautologie, da die Aussage A immer entweder wahr oder falsch ist.

In Zeichen: $\models A \or \neg A$

Beispiel: P ∨ ¬P (gesprochen: P oder nicht P), der Satz vom ausgeschlossenen Dritten

P ist ein beliebiger logischer Ausdruck, der die Wahrheitswerte WAHR (W) oder FALSCH (F) annehmen kann.

Beweis:

P	¬P	P ∨ ¬P
W	F	W
F	W	W

• Für jede Aussage A, B ist "A ist eine hinreichende Bedingung für B, oder B ist eine hinreichende Bedingung für A" eine Tautologie.

In Zeichen: $\models (A\rightarrow B)\or(B\rightarrow A)$

• Für alle Aussagen A, B, C ist "Wenn unter der Voraussetzung, dass A der Fall ist, B eine hinreichende Bedingung für C ist, dann ist die Tatsache, dass A eine hinreichende Bedingung für B ist, ausreichend dafür, dass A eine hinreichende Bedingung für C ist" eine Tautologie.

In Zeichen: $\models (A\rightarrow (B\rightarrow C))\rightarrow ((A\rightarrow B)\rightarrow (A\rightarrow C))$

Diese Aussagen gelten unabhängig davon, ob A, B und C selbst wahr ist oder nicht.

• In der Programmierung häufig falsch anzutreffen: WENN (varText 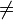$\ne$ "Hallo") ODER (varText 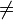$\ne$ "Guten Tag") DANN ...; wird für alle Wahrheitsmöglichkeiten den Wert WAHR liefern. Eine solche Aussage wird im täglichen Sprachgebrauch häufig mit einem oder gesprochen, gemeint ist aber das logische und (Konjunktion).

Tautologien in mehrwertigen Logiken

In mehrwertigen Logiken, also in nichtklassischen Logiken, die durch die Aufgabe des Prinzips der Zweiwertigkeit entstehen, verliert der Tautologiebegriff seine − vermeintliche oder tatsächliche − umgangssprachliche Natürlichkeit und muss neu definiert werden.

Eine Möglichkeit, den Tautologiebegriff in die mehrwertige Logik zu übernehmen, besteht darin, aus den Wahrheitswerten (im mehrwertigen Fall besser: Pseudowahrheitswerten oder Quasiwahrheitswerten) einen oder mehrere herauszugreifen und ihnen besondere Bedeutung zuzumessen. Diese herausgegriffenen Pseudowahrheitswerte werden designierte Pseudowahrheitswerte genannt. Man definiert, dass all jene Aussagen Tautologien sind, die für jede Bewertung der in ihnen vorkommenden Atome einen designierten Wahrheitswert liefern. Bei dieser Lösung bleibt der Tautologiebegriff selber zweiwertig, d. h., eine Aussage ist entweder eine Tautologie, oder sie ist keine.

Tautologietests

Von zentraler Bedeutung für die Logik sind Methoden, zu prüfen, ob Aussagen kontingent (also in ihrer Wahrheit von den Wahr- oder Falschheiten ihrer Grundbausteine abhängig) oder tautologisch (in jedem Fall wahr) sind.

Während eine solche Prüfung prinzipiell mithilfe jeder Methode möglich ist, mit der für alle möglichen Fälle die Wahr- oder Falschheit einer Aussage ermittelbar ist, nimmt die sog. Baummethode einen besonderen Stellenwert ein, da hier nicht jeder einzelne Fall geprüft werden muss.

Siehe auch

• Theorem, Kontradiktion, erfüllbare Aussage, Schlussregel, Zirkelschluss, Tautologie (Sprache), Allgemeingültigkeit, Antinomie
• Zirkelschluss, Idem per idem

Weblinks

• Webformular zur (zweiwertigen) Tautologieprüfung

Quellen

1. ↑ ein Aussageschema, eine Formel, ein Satz
2. ↑ Spies, Einführung in die Logik (2004), S. 16
3. ↑ Lohnstein, Formale Semantik (1996), S. 104
4. ↑ So Reichenbach, Grundzüge der symbolischen Logik (1999), S. 49
5. ↑ These 6.11 im Tractatus Logico-Philosophicus, zitiert nach Urchs, Klassische Logik (1993), S. 14 Fn. 2
6. ↑ Bocheński, Formale Logik, 2. Aufl. (1962), S. 387 f.
7. ↑ Regenbogen/Meyer, Wörterbuch der philosophischen Begriffe (2005)/Logik
8. ↑ Reichenbach, Grundzüger der symbolischen Logik (1999), S. 35
9. ↑ Vgl. „Tautologie sind semantisch durchaus sinnvoll. Wir sind geradezu aus auf Tautologien, wenn wir eine Definition oder Worterklärung vornehmen. Dann lernen wir aus der Tautologie die Bedeutung eines Wortes. Allerdings setzt dies eine gewisse syntaktische Form voraus, nämlich die Äquivalenz, die Identitätsaussage oder auch eine generelle Prädikation.“ Wunderlich, Arbeitsbuch Semantik, 2. Aufl. (1991), S.118

Literatur

• Joseph M. Bochenski: Formale Logik. 4. Auflage 1978, Verlag Karl Alber, Freiburg, München 1956.
• Lothar Kreiser, Siegfried Gottwald, Werner Stelzner (Hrsg.): Nichtklassische Logik. Eine Einführung. Akademie ², Berlin 1990.
• Markus Spieß: Einführung in die Logik. Werkzeuge für Wissensrepräsentation und Wissensmanagement. Spektrum-Akademischer Verlag, 2003, ISBN 9783827413796.