Bessel-Punkt

Die Bessel-Punkte (nach Friedrich Wilhelm Bessel) sind die optimalen Positionen der Auflager eines gleichmäßig belasteten Balkens oder Bretts.

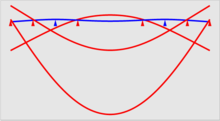Verbiegung (stark überhöht) eines gleichmäßig belasteten Balkens für verschiedene Paare von Auflagepunkten; blau: Lagerung in den Bessel-Punkten

Man betrachtet einen horizontalen Balken der Länge L, der sich unter seinem eigenen Gewicht oder dem einer gleichmäßig verteilten Last elastisch verbiegt. Ein anschauliches Anwendungsbeispiel ist ein mit Büchern belasteter Regalboden. Es sollen zwei symmetrische Auflagepunkte gewählt werden, die bei x und L − x liegen.

Aus der Differentialgleichung für den schwach gebogenen Stab findet man verschiedene Lösungen, je nachdem, welche Deformation man für optimal erklärt:

Drehmomentenfreie Lagerung

Der elastisch verformte Balken soll in den Auflagerpunkten eine horizontale Tangente aufweisen und kein Drehmoment auf die Lager ausüben. Dann findet man

$x/L=\sqrt{3/2}-1 \approx 0{,}2247$.

Die mittlere Durchbiegung des Biegeträgers nimmt in diesem Fall ein Minimum an; sie ist um den Faktor 65,3 kleiner als der entsprechende Wert bei Lagerung an den beiden Enden des Balkens.

Ob die drehmomentenfreie Lagerung historisch korrekt als Bessel-Punkt-Lagerung bezeichnet werden kann, müsste noch geklärt werden.

Airy-Punkte

Als Airy-Punkte bezeichnet man die Auflagerpositionen, die zu einem horizontalen Verlauf der Biegelinie an den Balkenenden führen. Sie liegen bei

$x/L\approx 0{,}2213$.

Normative Festlegung

In Normen der Längenmesstechnik werden die Besselschen Punkte als Auflagepunkte, die zur geringsten Durchbiegung des Balkens führen, definiert. Hierbei ist der Betrag der Durchbiegung an den Enden des Balkens gleich der Durchbiegung in der Mitte. Sie liegen bei

$x/L\approx 0{,}2232$.

Die Wahl der Auflagepunkte hat in der Präzisionsmessung z. B. mit langen Montagelinealen oder Messbalken einen entscheidenden Einfluss auf das Messergebnis.

Weblinks

• Optimale Lagerung (PDF; 564 kB)