Bildschirmdiagonale

Die Bildschirmdiagonale ist ein Maß für die Größe eines Bildschirms. Sie bezeichnet den Abstand zwischen zwei sich diagonal gegenüberliegenden Ecken.

Die Angabe der Bildschirmdiagonale ist nur beschränkt zweckmäßig. Der Vorteil einer einzigen Maßzahl gegenüber der gemeinsamen Angabe von Breite und Höhe kann nur dann genutzt werden, wenn alle Geräte einer Klasse dasselbe Bildseitenverhältnis aufweisen, wie es lange Zeit bei Fernsehgeräten üblich war. Gegenüber der Angabe der Bildfläche bietet die Diagonale den Vorteil, dass sie sich durch eine einzige Messung und ohne Rechnung ermitteln lässt.

In der Werbung wird die Bildschirmdiagonale insbesondere bei Computermonitoren und Flüssigkristallanzeigen häufig in Zoll angegeben und ist üblicherweise eine runde Maßzahl und nicht ein gemessener Wert. Siehe auch DPI.

Verwendung nach Technik

Bei Kathodenstrahlröhrengeräten (CRT) erfolgt die Angabe der Bildschirmdiagonalen üblicherweise zweiteilig als physische und sichtbare Bilddiagonale, da aus technischen Gründen ein Teil der Röhre immer verdeckt ist. Wenn nur ein Wert angegeben ist, ist normalerweise die physische Diagonale gemeint.

Da bei der Größenangabe von Röhrenmonitoren nicht die sichtbare Diagonale, sondern die Gesamtgröße der (teils nicht sichtbaren) Röhre ausschlaggebend war, ist der Vergleichswert gegenüber Flachbildschirmen in der Regel um etwa zwei Zoll zu reduzieren. Ein 19-Zoll CRT entspricht also etwa einem 17-Zoll TFT.

Verwendung nach Geräteklasse

Fernseher

Handelsübliche Fernsehgeräte liegen überwiegend im Bereich von 30 cm bis 110 cm, wobei die größten klassischen Röhrenapparate nur etwa 85 cm sichtbare Bildschirmdiagonale erreichen. Die Angabe wird ebenfalls auf Projektionsleinwände angewendet, die höhere Werte aufweisen. Das klassische Seitenverhältnis beträgt 4:3, aber zunehmend mehr Geräte bieten 16:9 oder 16:10.

Computermonitore

Die meisten Computermonitore weisen eine Bildschirmdiagonale zwischen 48 und 71 Zentimeter (19 in bis 28 in) auf, wobei die Nachfrage nach größeren Geräten kontinuierlich steigt. Tragbare (7 in bis 15 in) und alte (14 in bis 17 in) Modelle sind mitunter auch kleiner, während für professionelle, grafikorientierte Anwendungen (DTP, CAD) auch größere Geräte verwendet werden. Traditionell war das Fernsehseitenverhältnis 4:3 üblich, doch neben dem eher quadratischen 5:4 werden breitere Formate wie 16:9, 16:10, 15:10 (3:2) immer häufiger, da sie eher dem natürlichen Blickfeld des Menschen entsprechen.

Kleingeräte

Daneben gibt es Geräte mit Bildschirmdiagonalen unterhalb von 30 cm (12 in), z. B. Mobiltelefone, PDAs, Hifi-Anlagen usw., die aus Energie-, Platz- oder Preisgründen keine größeren Anzeigen haben oder brauchen.

Geometrie

Seitenlängen und Fläche

Bildschirmbreite und -höhe in Abhängigkeit von der Diagonalen

Typische Bildschirmgrößen und Geometrieparameter im Vergleich

Ist das Bildseitenverhältnis (a:b, z. B. 4:3 oder 16:9) bekannt, lassen sich gemäß dem Satz des Pythagoras mit der Diagonalen (d) die Seitenlängen (w, h) sowie die Bildfläche (A) berechnen:

$\begin{align} w &= \tfrac{a}{\sqrt{a^2 + b^2}} \cdot d\\ h &= \tfrac{b}{\sqrt{a^2 + b^2}} \cdot d\\ A &= \tfrac{a \cdot b}{a^2 + b^2} \cdot d^2 \end{align}$

So hat bspw. ein 4:3-Bildschirm mit 50 cm Diagonale eine horizontale Seite von 40 cm (= ⁴⁄₅ · 50 cm) und eine vertikale Seite von 30 cm (= ³⁄₅ · 50 cm), somit eine Fläche von 12 dm² (= ¹²⁄₂₅ · 2500 cm² = 40 cm × 30 cm).

Pixel

Die Größe eines Bildschirmpunktes (P) lässt sich bei bekannter Auflösung (W = x, H = y) entsprechend bestimmen:

quadratische Pixel

$\frac W H = \frac a b$

$P_x = P_y = \frac{1}{\sqrt{W^2 + H^2}} \cdot d$

allgemein

$P_x = \frac{a}{\sqrt{a^2 + b^2} \cdot W} \cdot d$

$P_y = \frac{b}{\sqrt{a^2 + b^2} \cdot H} \cdot d$

$N_P = P_x \cdot P_y$

Der genannte Bildschirm mit 50 cm Diagonale hätte also bei einer Auflösung von 1280 px × 960 px (= 1,23 Mpx) quadratische Bildpunkte mit einer theoretischen Kantenlänge von ⁵⁄₁₆ Millimetern oder 312,5 Mikrometern, das entspricht 81,3 px/in (DPI).

Ist die Diagonale gegeben, erhält man die Bildauflösung (R), also die Anzahl der Punkte pro Längeneinheit (z.B. dots per inch, dpi), durch eine inverse Operation:

quadratische Pixel

$\frac W H = \frac a b$

$R_x = R_y = \frac{\sqrt{W^2 + H^2}}{d}$

allgemein

$R_x = \frac{\sqrt{a^2 + b^2} \cdot W}{a \cdot d}$

$R_y = \frac{\sqrt{a^2 + b^2} \cdot H}{b \cdot d}$

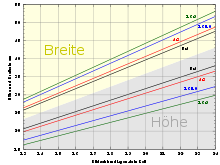
Bei zwei Geräten mit unterschiedlichem Seitenverhältnis (a₁:b₁ und a₂:b₂), müssen sich die Diagonalen (d₁ und d₂) unterscheiden, um ein Bild mit gleicher Höhe (h) oder Breite (w) darzustellen:

gleiche Höhe

h₂ = h₁

$d_2 = d_1 \cdot \frac{b_1}{b_2} \cdot \sqrt{\frac{a_2^2 + b_2^2}{a_1^2 + b_1^2}}$

gleiche Breite

w₂ = w₁

$d_2 = d_1 \cdot \frac{a_1}{a_2} \cdot \sqrt{\frac{a_2^2 + b_2^2}{a_1^2 + b_1^2}}$

Werte

Die Berechnung der Tabelle erfolgt aus der Diagonalen und dem Seitenverhältnis. Die Längen sind auf zwei, die Flächen auf drei Stellen gerundet.

Diagonale			4:3 = 16:12 = 12:9				16:9				8:5 = 16:10				5:4 = 15:12
(in)	(cm)		w (cm)	h (cm)	A (dm²)		w (cm)	h (cm)	A (dm²)		w (cm)	h (cm)	A (dm²)		w (cm)	h (cm)	A (dm²)
1	2,5		2,0	1,5	0,03		2,2	1,3	0,03		2,2	1,4	0,03		2,0	1,6	0,03
2	5,1		4,1	3,0	0,12		4,4	2,5	0,11		4,3	2,7	0,12		4,0	3,2	0,13
3	7,6		6,1	4,6	0,28		6,6	3,7	0,25		6,5	4,0	0,26		6,0	4,8	0,28
3,5	8,9		7,1	5,3	0,38		7,7	4,4	0,34		7,5	4,7	0,36		6,9	5,6	0,39
4	10		8,1	6,1	0,50		8,9	5,0	0,44		8,6	5,4	0,46		7,9	6,3	0,50
5	13		10	7,6	0,77		11	6,2	0,69		11	6,7	0,73		10	7,9	0,79
6	15		12	9,1	1,11		13	7,5	0,99		13	8,1	1,04		12	10	1,13
7	18		14	11	1,52		15	8,7	1,35		15	9,4	1,42		14	11	1,54
8	20		16	12	1,98		18	10	1,76		17	11	1,86		16	13	2,01
9	23		18	14	2,51		20	11	2,23		19	12	2,35		18	14	2,55
10	25		20	15	3,10		22	12	2,76		22	14	2,90		20	16	3,15
10,1	26		21	15	3,16		22	13	2,81		22	14	2,96		20	16	3,21
11	28		22	17	3,75		24	14	3,34		24	15	3,51		22	17	3,81
12	30		24	18	4,46		27	15	3,97		26	16	4,18		24	19	4,53
13	33		26	20	5,23		29	16	4,66		28	18	4,90		26	21	5,32
13,3	34		27	20	5,48		29	17	4,88		29	18	5,13		26	21	5,57
14	36		28	21	6,07		31	17	5,40		30	19	5,68		28	22	6,17
15	38		30	23	6,97		33	19	6,20		32	20	6,52		30	24	7,08
15,4	39		31	23	7,34		34	19	6,54		33	21	6,88		31	24	7,46
16	41		33	24	7,93		35	20	7,06		34	22	7,42		32	25	8,06
17	43		35	26	8,95		38	21	7,97		37	23	8,38		34	27	9,10
18	46		37	27	10,0		40	22	8,93		39	24	9,39		36	29	10,2
19	48		39	29	11,2		42	24	9,95		41	26	10,5		38	30	11,4
20	51		41	30	12,4		44	25	11,0		43	27	11,6		40	32	12,6
21	53		43	32	13,7		46	26	12,2		45	28	12,8		42	33	13,9
22	56		45	34	15,0		49	27	13,3		47	30	14,0		44	35	15,2
23	58		47	35	16,4		51	29	14,6		50	31	15,3		46	36	16,6
24	61		49	37	17,8		53	30	15,9		52	32	16,7		48	38	18,1
25	64		51	38	19,4		55	31	17,2		54	34	18,1		50	40	19,7
26	66		53	40	20,9		58	32	18,6		56	35	19,6		52	41	21,3
27	69		55	41	22,6		60	34	20,1		58	36	21,1		54	43	22,9
28	71		57	43	24,3		62	35	21,6		60	38	22,7		56	44	24,7
29	74		59	44	26,0		64	36	23,2		62	39	24,4		58	46	26,5
30	76		61	46	27,9		66	37	24,8		65	40	26,1		60	48	28,3
32	81		65	49	31,7		71	40	28,2		69	43	29,7		63	51	32,2
37	94		75	56	42,4		82	46	37,7		80	50	39,7		73	59	43,1
40	102		81	61	49,5		89	50	44,1		86	54	46,4		79	63	50,4
42	107		85	64	54,6		93	52	48,6		90	57	51,1		83	67	55,5
46	117		93	70	65,5		102	57	58,3		99	62	61,4		91	73	66,6
52	132		106	79	83,7		115	65	74,5		112	70	78,4		103	83	85,1
55	140		112	84	93,7		122	68	83,4		118	74	87,7		109	87	95,2
60	152		122	91	111		133	75	99,2		129	81	104		119	95	113
65	165		132	99	131		144	81	116		140	88	123		129	103	133
70	178		142	107	152		155	87	135		151	94	142		139	111	154
75	191		152	114	174		166	93	155		162	101	163		149	119	177
80	203		163	122	198		177	100	176		172	108	186		159	127	201
85	216		173	130	224		188	106	199		183	114	209		169	135	228
90	229		183	137	251		199	112	223		194	121	235		179	143	255
95	241		193	145	279		210	118	249		205	128	262		188	151	284
100	254		203	152	310		221	125	276		215	135	290		198	159	315
105	267		213	160	341		232	131	304		226	141	320		208	167	347
110	279		224	168	375		244	137	334		237	148	351		218	175	381
115	292		234	175	410		255	143	365		248	155	383		228	182	416
120	305		244	183	446		266	149	397		258	162	418		238	190	453

Vergleich mit Papier

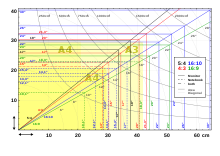
Eine A4-Papierseite (297 mm × 210 mm) hat eine Diagonale von 364 mm (14,3 in) bei einem Seitenverhältnis von √2 ≈ 1,414, d.h. zwischen 4:3 und 16:10. Eine A3-Seite ist doppelt (420 mm × 297 mm), A5 halb so groß (210 mm × 148 mm). Das amerikanische Letter-Format ist von ähnlicher Größe wie A4: 11 in × 8,5 in = 279 mm × 216 mm, Diagonale 13,9 in = 353 mm.

kleinste Bildschirmdiagonalen (in Zoll), auf denen gängige Papierformate dargestellt werden können

	quer				hoch
Papier	5:4	4:3	8:5	16:9	5:4	4:3	8:5	16:9
A5	11	11	11	12	14	14	16	17
A4	15	15	16	17	19	20	22	24
Letter	15	15	17	18	18	19	21	23
2 Letter					22	22	21	23
A3	22	21	22	24	27	28	32	34

Weblinks

 Wiktionary: Bildschirmdiagonale – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen