Gleitender Mittelwert

Der gleitende Mittelwert wird auch gleitender Durchschnitt genannt. Gleitende Mittelwerte verringern die in einer Datenreihe vorhandene Variation. Daher werden sie oft verwendet, um Zeitreihen zu glätten. In der Signalverarbeitung sind gleitende Durchschnitte Tiefpassfilter, sie dämpfen vor allem hohe Frequenzen.

Einfacher gleitender Mittelwert

Zentrierte gleitende Mittelwerte der Ordnung 3

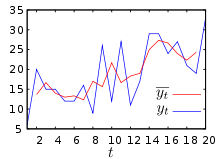
Bei einer gegebenen Menge von Zahlen (Datenpunkten), in der Regel Zeitreihen y1, y2, ..., definiert man einen gleitenden Mittelwert $\bar y_t$ der Ordnung n als Folge der arithmetischen Mittelwerte aufeinanderfolgender Datenpunkte.

Zentrierter gleitender Mittelwert

Ein einfaches Beispiel ist der zentrierte gleitende Mittelwert der Ordnung 3:

$\bar y_{2}= \frac{y_1 + y_2 + y_3}{3} \;,\quad \bar y_{3}= \frac{y_2 + y_3 + y_4}{3} \;,\;\cdots$

Allgemein ergibt sich für eine ungeradzahlige Ordnung n die Folge

$\bar y_{\frac{n+1}{2}}= {y_1 + y_2 + \cdots + y_{\frac{n+1}{2}} \cdots + y_n \over n } \; ,$

$\bar y_{\frac{n+1}{2}+1}= { y_2 + y_3 + \cdots + y_{\frac{n+1}{2}+1} \cdots + y_{n+1} \over n } \; ,$

$\cdots$

Der Zeitreihenwert in der Mitte der Zählersumme gibt den Index t für $\bar y_t$ vor. Für die ersten und letzten $\frac{n-1}{2}$ Zeitreihenwerte liegt also kein gleitender Durchschnittswert vor.

Spektrale Eigenschaften

Filterfunktion des zentrierten gleitenden Mittelwerts 3-ter Ordnung

Bildet man den zentrierten gleitenden Mittelwert n-ter Ordnung $\bar X^{(n)}$ einer schwachstationären Zeitreihe X_t mit Spektraldichte f_X, dann hat $\bar X^{(n)}$ die gefilterte Spektraldichte

$|\varphi(\omega)|^2\cdot f_X(\omega)$

mit der Filterfunktion

$|\varphi(\omega)|^2 := \frac{2\pi}n k_n(\omega)$,

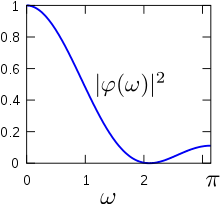
wobei k_n den Fejér-Kern bezeichnet. An der grafischen Darstellung für n = 3 kann man die Tiefpass-Eigenschaft erkennen, wo Frequenzen nahe 0 ungehindert passieren. ^[1].

Einseitiger gleitender Mittelwert

Bei Zeitreihen ist der zentrierte gleitende Mittelwert vorgreifend (ein nicht kausaler Filter), d.h. für die Berechnung von $\bar y_t$ zum Zeitpunkt t werden Werte $\bar y_{t+1}$ usw. aus der Zukunft von t benötigt, die oft nicht seriös abgeschätzt werden können.

Deswegen betrachtet man auch die einseitigen gleitenden Mittelwerte, die nur Werte aus der Vergangenheit von t verwenden.

Der einseitige gleitende Mittelwert zur Ordnung 3 ist entsprechend definiert als

$\bar y_{3}= \frac{y_1 + y_2 + y_3}{3} \;,\quad \bar y_{4}= \frac{y_2 + y_3 + y_4}{3} \;,\;\cdots$,

wobei der jüngste Zeitreihenwert den Index für $\bar y_t$ vorgibt.
Ein Beispiel für die Verwendung von einseitigen gleitenden Mittelwerten sind die üblichen 38- bzw. 200-Tage-Durchschnittswerte von Börsenkursen, die den gleitenden Mittelwert der vergangenen x Börsentage eines Wertpapierkurses beschreiben.

Gewichteter gleitender Mittelwert

Ein gewichteter gleitender Mittelwert ordnet den Datenpunkten Gewichte zu. Bei einem gewichteten Mittelwert im engeren Sinn sind diese Gewichte arithmetisch abnehmende Werte.
Für den gewichteten gleitenden Mittelwert der Ordnung N erhält der jüngste Datenpunkt y_N das Gewicht "n", der vorletzte "n-1", etc.

$\bar y_{N}={ n y_N + (n-1) y_{N-1} + \cdots + 2 y_{N-n+2} + y_{N-n+1} \over n + (n-1) + \cdots + 2 + 1} = \frac{2(n y_N + (n-1) y_{N-1} + \cdots + 2 y_{N-n+2} + y_{N-n+1})}{n(n+1)}$

d.h. jüngere Datenpunkte werden stärker gewichtet als weiter zurückliegende.

Exponentiell geglätteter Mittelwert

Der exponentiell geglättete Mittelwert ordnet den Datenpunkten einer Zeitreihe exponentiell abnehmende Gewichte zu. Somit werden auch hier jüngere Datenpunkte stärker gewichtet als weiter zurückliegende, jedoch noch stärker als beim gewichteten gleitenden Mittelwert.

Vergleich mit Digitalfilter

Ein gleitender Mittelwert kann auch als digitales Filter interpretiert werden, dann stellt es grundsätzlich einen Tiefpass dar.

• Der einfache gleitende Mittelwert (engl.: Simple Moving Average (SMA)) entspricht einem FIR-Filter mit N Filterkoeffizienten $b_i = {1 \over N}, i \in 0 \dots N-1$ (und a₀ = 1).

• Beim linear gewichteten gleitenden Mittelwert (engl.: (Linear) Weighted Moving Average ((L)WMA) steigen die Filterkoeffizienten linear an: $b_{i-1} = {i \over \sum_{k=1}^N k}, i \in 1 \dots N$ (und a₀ = 1).

• Der exponentiell geglättete Mittelwert (engl.: Exponential Moving Average (EMA)) entspricht einem IIR-Filter 1. Ordnung mit den Filterkoeffizienten b₀ = α und a₀ = 1, a₁ = − (1 − α) mit dem Parameter $0 \leq \alpha \leq 1$.

Siehe auch

• ARMA-Modell

Einzelnachweise

1. ↑ Jens-Peter Kreiß, Georg Neuhaus: Einführung in die Zeitreihenanalyse. Springer, 2006. ISBN 978-3-540-25628-1

Weblinks

•  Wikibooks: Gleitende Durchschnitte – Lern- und Lehrmaterialien