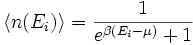Fermi-Dirac-Verteilung

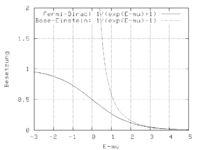Illustration der Besetzung $\langle n(E)\rangle$ (siehe Bose-Einstein-Statistik) für Bosonen (obere Kurve) bzw. Fermionen (untere Kurve) im Spezialfall der Wechselwirkungsfreiheit. Das sog. chemische Potenzial µ ist im Fermifall positiv, bei T = 0K entspricht es der Fermienergie; im Bose-Fall ist es dagegen ein negativer Parameter, der in bestimmter Weise von Temperatur und Dichte abhängt und im Grenzfall der Bose-Einstein-Kondensation verschwinden würde.

Die Fermi-Dirac-Statistik ist wie die Bose-Einstein-Statistik eine wichtige Form der allgemeinen Quantenstatistik. Erstere nimmt diese Form an für Teilchen mit halbzahligem Spin (Fermionen), während sich bei ganzzahligem Spin die sog. Bose-Einstein-Statistik ergibt. (Man unterscheidet Fermionen bzw. Bosonen, je nachdem ob der Spin des Teilchens – in Einheiten von 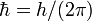$\hbar =h/(2\pi)$, mit dem Wirkungsquantum h – einen der halbzahligen Werte 1/2, 3/2, 5/2, ... bzw. einen der ganzzahligen Wert, 0, 1, 2, ..., annimmt. Andere Fälle gibt es nicht.)

Kernpunkt der Fermi-Dirac-Statistik ist, dass bei halbzahligem Spin die Wellenfunktion (oder der „Zustandsvektor“) eines Vielteilchensystems bezüglich gleichzeitiger Vertauschung aller vier Argumente x, y, z, m bei zwei Teilchen (wobei x, y, und z drei Ortvariable und m die sogenannte Spinvariable des Teilchens ist) das Vorzeichen wechselt 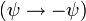$(\psi \rightarrow -\psi)$, während sich bei Bosonen dieselbe Wellenfunktion ergeben würde 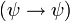$(\psi \rightarrow \psi)$. Im wichtigen Spezialfall der Wechselwirkungsfreiheit ergibt sich für Fermionen die Fermiverteilung; bei Bose-Teilchen kommt es dagegen unter Umständen zur Komplikation der Bose-Einstein-Kondensation, für die es bei Fermionen kein Analogon gibt.

Die Fermi-Dirac-Statistik hängt mit dem sogenannten Pauli-Prinzip zusammen, das anschaulich besagt, dass zwei in allen vier Argumenten (s.o.) identische Fermionen niemals zum gleichen Gesamtzustand eines Systems beitragen können, da in diesem Fall Vertauschung zweier Teilchen (gleichzeitige Vertauschung aller vier Argumente!) offenbar keine Auswirkungen hätte. Etwas weniger anschaulich folgt dies genau aus der obigen Forderung nach Vorzeichenwechsel der Wellenfunktion, welche sich wiederum aus dem ungewöhnlichen Drehverhalten der Wellenfunktion einzelner Fermionen ergibt (bei einer Drehung um 360^o ändert diese im Fermi-Fall ihr Vorzeichen, entsprechend einer gewöhnlichen Drehung um nur 180^o, im Bose-Fall reproduziert sie sich).

Die Tatsache, dass Teilchen mit halbzahligem Spin der Fermi-Dirac-Statistik folgen, bezeichnet man auch als Spin-Statistik-Theorem. Es folgt aus den Grundannahmen der relativistischen Quantenfeldtheorie und wurde ebenfalls von Wolfgang Pauli bewiesen.

Die mittlere Besetzungszahl durch Fermionen innerhalb eines Systems bei einer bestimmten Energie E_i wird folgendermaßen beschrieben:

$\langle n(E_i) \rangle = \frac {1}{e^{\beta (E_i - \mu)} + 1}$

Hierbei ist μ das chemische Potenzial (welches bei T = 0K der Fermi-Energie entspricht) und β die Energienormierung. Diese wird üblicherweise zu 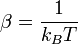$\beta=\frac {1}{k_{B} T}$ gewählt (mit der Boltzmann-Konstanten k_B und der absoluten Temperatur T).

Betrachtet man entartete Energieniveaus, so taucht sowohl bei der Fermi-Dirac-Statistik als auch bei der Bose-Einstein-Statistik ein sogenannter Entartungsfaktor g=2s+1 auf. Für Fermionen mit s=1/2 ist dieser g=2.

Für den Grenzfall sehr großer Energien gehen sowohl die Fermi-Dirac-Statistik als auch die Bose-Statistik in die klassische Boltzmann-Statistik über.

Literatur

• U. Krey, A. Owen, Basic Theoretical Physics - a Concise Overview, Berlin Heidelberg New York, Springer 2007, (in Englisch) , ISBN 978-3-540-36804-5

Siehe auch

• Fermiverteilung
• Bose-Einstein-Statistik
• Fermi-Dirac-Integral
• Anyon