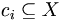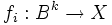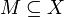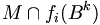CW-Komplex

In der Topologie, einem der Teilgebiete der Mathematik, bezeichnet der Begriff Komplex einen topologischen Raum, der aus einfachen Bestandteilen wie Punkten, Strecken, Dreiecken, Tetraedern etc. zusammengesetzt ist. Dabei werden die Bestandteile sinnvoll "zusammengeklebt", d.h. Punkte sind Endpunkte von Strecken, Strecken sind Seiten von Dreiecken, Dreiecke sind Seitenflächen von Tetraedern. Dabei kann ein einzelner Punkt mit Endpunkten verschiedener Strecken identifiziert werden, in einem Tetraeder ist jede Strecke eine Seite von zwei Seitenflächen usw. Es können auch kompliziertere Gebilde zusammengesetzt werden, so kann ein Viereck in zwei Dreiecke mit gemeinsamer Kante zerlegt werden.

Allgemein werden Gebilde in topologischen Räumen in Teile zerlegt, die zu diesen einfachen Figuren homöomorph sind. So kann man die Oberfläche eines Torus oder einer "Brezel" mit einem Netz aus Dreiecken überdecken und die Eigenschaften des so entstandenen Graphen untersuchen. Auch können die Graphen zu verschiedenen Dreieckszerlegungen derselben Fläche auf gemeinsame Eigenschaften untersucht werden.

Simplizialkomplex

Ein Simplizialkomplex K zu einer Menge M ist eine Teilmenge der Potenzmenge 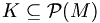$K \subseteq \mathcal P(M)$, (d.h. eine Menge von Teilmengen), die unter Bildung von Mengendurchschnitten abgeschlossen ist.

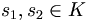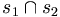Geometrisch ist ein Simplizialkomplex K eine Menge von Simplexen, so dass die leere Menge und alle Seiten von Simplexen in K enthalten sind, und für $s_1 , s_2 \in K$ gilt: $s_1 \cap s_2$ ist Seite von 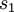$s_1\$ und $s_2\$.

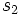Zell-Komplex

Eine k-Zelle ist ein topologischer Raum, der zu B^k homöomorph ist. Eine offene k-Zelle ist ein topologischer Raum, der zum Inneren von B^k homöomorph ist. k nennt man die Dimension der Zelle.

Ein Zell-Komplex oder auch CW-Komplex (closure-finite weak-topology) ist ein Hausdorff-Raum X, der in offene Zellen 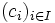$(c_i)_{i \in I}$ zerfällt, wobei gilt:

1. zu jeder k-Zelle $c_i \subseteq X$ existiert eine charakteristische Abbildung $f_i: B^k \rightarrow X$ so dass das Innere von B^k homöomorph auf c_i und der Rand in eine Vereinigung von endlich vielen Zellen der Dimension < k stetig abgebildet wird.
2. $M \subseteq X$ ist genau dann abgeschlossen, wenn $M \cap f_i(B^k)$ für alle $i \in I$ abgeschlossen ist.