- Hausdorff-Raum
-
Ein Hausdorff-Raum (auch hausdorffscher Raum) (nach Felix Hausdorff) oder separierter Raum ist ein topologischer Raum M, in dem das Trennungsaxiom T2 (auch Hausdorffeigenschaft oder Hausdorff'sches Trennungsaxiom genannt) gilt.
Inhaltsverzeichnis
Definition
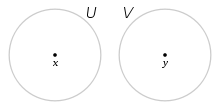
Ein topologischer Raum M hat die Hausdorffeigenschaft, wenn für alle x,y aus M mit
 disjunkte offene Umgebungen U(x) und V(y) existieren.
disjunkte offene Umgebungen U(x) und V(y) existieren.Mit anderen Worten: alle paarweise verschiedenen Punkte x und y aus M werden durch Umgebungen getrennt. Ein topologischer Raum, der die Hausdorffeigenschaft erfüllt, wird Hausdorff-Raum genannt.
Einordnung in die Hierarchie topologischer Räume
Ein topologischer Raum ist genau dann ein Hausdorff-Raum, wenn er präregulär (R1) ist:
- alle paarweise topologisch unterscheidbaren Punkte x und y aus M werden durch Umgebungen getrennt,
und die Kolmogoroff-Eigenschaft (T0) besitzt:
- alle paarweise verschiedenen Punkte x und y aus M sind topologisch unterscheidbar.
Topologisch unterscheidbar heißen zwei Punkte x und y genau dann, wenn es eine offene Menge gibt, die den einen Punkt enthält, den anderen aber nicht.
Beweis:
- Wenn R1 und T0 gegeben sind, folgt unmittelbar T2: diesen Schluss kann man rein formal ziehen, ohne zu wissen, was topologisch unterscheidbar überhaupt heißt.
- Der umgekehrte Schluss von T2 auf R1 und T0 geht so:
- Aus der Definition von T2 folgt für verschiedene x, y die Existenz der Menge U(x), die x, aber nicht y enthält, ergo gilt T0.
- Seien x, y zwei topologisch unterscheidbare Punkte: dann gibt es eine Menge, die den einen Punkt enthält, den anderen aber nicht; somit ist x≠y. Dann folgt mit T2, dass x und y durch Umgebungen getrennt sind. Ergo gilt R1.
Spezialisierung
Ein Hausdorff-Raum, der zusätzlich noch normal ist, wird als T4-Raum bezeichnet.
Beispiele
Insbesondere sind in topologischen Hausdorff-Räumen Grenzwerte – anders als in allgemeinen topologischen Räumen – eindeutig.
So gut wie alle in der Analysis betrachteten Räume sind Hausdorff-Räume. Insbesondere ist jeder metrische Raum ein Hausdorff-Raum.
Ein Beispiel für einen Hausdorff-Raum, der kein metrischer Raum ist, ist die Menge der abzählbaren Ordinalzahlen mit der gewöhnlichen Ordnungstopologie.
Wird das Spektrum eines Ringes mit der Zariski-Topologie versehen, erhält man einen nüchternen topologischen Raum, der meist nicht präregulär, geschweige denn hausdorffsch ist.
Akademischer Humor
Im Gebäude des mathematischen Instituts der Universität Bonn, an der Felix Hausdorff jahrelang lehrte und forschte, gibt es einen Raum, der als „Hausdorff-Raum“ bezeichnet wird.
Literatur
- Boto von Querenburg: Mengentheoretische Topologie. 3. neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2001, ISBN 3-540-67790-9 (Springer-Lehrbuch).
Wikimedia Foundation.