Borsuk-Vermutung

Die Borsuk-Vermutung ist eine mathematische Vermutung aus dem Bereich der Geometrie. Es geht dabei um die Frage, in wie viele Teile man eine gegebene Menge beschränkten Durchmessers zerlegen muss, damit jeder Teil einen echt kleineren Durchmesser hat. Die 1933 von Karol Borsuk aufgestellte, nahe liegende Vermutung, dass man in n Dimensionen mit n + 1 Teilen auskommt, hat sich als falsch erwiesen.

Eine Strecke, ein Dreieck und ein Tetraeder können in 2,3 bzw. 4 kleinere Teile zerlegt werden.

Die Vermutung

Im n-dimensionalen Raum $\R^n$ kann mittels der euklidischen Norm der Durchmesser einer Menge $E\subset \R^n$ als $\sup\{\|x-y\|; \, x,y\in E \}$ (maximaler Abstand zweier Punkte der Menge) definiert werden.

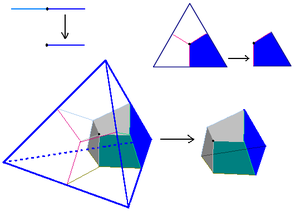
Man kann nun versuchen, die Menge E so in Teilmengen $E=E_1\cup\ldots \cup E_k$ zu zerlegen, dass jeder Teil E_i einen echt kleineren Durchmesser als E hat. Es stellt sich die Frage, wie viele Teilmengen E_i dazu erforderlich sind.

Wie das regelmäßige, n-dimensionale Simplex zeigt, sind im Allgemeinen mindestens n + 1 Mengen erforderlich, denn die n + 1 Ecken haben alle denselben Abstand, der gleich dem Durchmesser ist. Eine Teilmenge echt kleineren Durchmessers kann daher höchstens eine Ecke enthalten, das heißt man benötigt mindestens so viele Teilmengen, wie es Ecken gibt, und davon hat man n + 1. Wie nebenstehende Zeichnung für die Dimensionen 1,2 und 3 deutlich macht, kommt man beim Simplex tatsächlich mit n + 1 Teilmengen aus. Karol Borsuk schloss seine Arbeit "Drei Sätze über die n-dimensionale Sphäre", in der er sich mit der Zerlegung von Kugeln beschäftigte, wie folgt^[1]:

Die folgende Frage bleibt offen: Lässt sich jede beschränkte Teilmenge E des Raumes Rⁿ in (n+1) Mengen zerlegen, von denen jede einen kleineren Durchmesser als E hat?

Die Vermutung, dass diese Frage zu bejahen sei, wurde als Borsuk-Vermutung bekannt und blieb 60 Jahre lang offen.

Widerlegung

Im Anschauungsraum $\R^3$ hatte sich die Vermutung 1955 bestätigt^[2]. Es mag daher überraschen, dass sich die Borsuk-Vermutung in höheren Dimensionen als falsch erweist. 1993 haben Jeff Kahn und G. Kalai gezeigt^[3], dass man für genügend große Dimensionen n mindestens $(1,1)^\sqrt{n}$ Teilmengen benötigt, womit die Borsuk-Vermutung widerlegt war, denn $(1,1)^\sqrt{n}$ wächst schneller als n + 1. Ein konkretes Gegenbeispiel wurde von A. Nilli im 964-dimensionalen Raum gefunden^[4]. Heute ist bekannt, dass die Borsuk-Vermutung für Dimensionen ab 298 falsch ist^[5]. Die Frage nach der kleinsten Dimension, ab der die Borsuk-Vermutung nicht mehr zutrifft, ist offen.

Einzelnachweise

1. ↑ K. Borsuk: Drei Sätze über die n-dimensionale Sphäre, Fundamenta Mathematica (1933), Band 20, Seiten 177-190
2. ↑ H. G. Eggleston: Covering a three-dimensional set with sets of smaller diameter, J. London Math. Society (1955), Band 30, Seiten 11-24
3. ↑ Kahn, Kalai A Counterexample to Borsuks conjecture, Bulletin American Mathematical Society, Bd. 29, 1993, S.60-62
4. ↑ A. Nilli: On Borsuk's problem, Jerusalem Combinatorics '93, Contemporary Mathematics 178, AMS 1994, Seiten 209-210
5. ↑ A. Hinrichs and C. Richter: New sets with large Borsuk numbers, Discrete Math. (2003), Band 270, Seiten 137-147

Quellen

Eine Darstellung dieses Themas findet sich in

• M. Aigner, G.M. Ziegler: Das BUCH der Beweise Springer, Berlin 2002, ISBN 3-540-42535-7 (3. Auflage: ISBN 978-3-642-02258-6), Kapitel 16