Strecke (Geometrie)

Historische Abbildung über die Konstruktion von Strecken (1699)

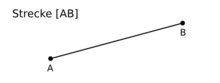
Eine Strecke (auch Geradenabschnitt oder Geradenstück) ist eine gerade Linie, die von zwei Punkten begrenzt wird; sie ist die kürzeste Verbindung ihrer beiden Endpunkte. Die Begrenzung einer Strecke durch diese Punkte unterscheidet sie von Geraden, die sich beidseitig ins Unendliche erstrecken, und von Strahlen (Halbgeraden), die auf einer Seite begrenzt sind.

Die in der Skizze verwendete Schreibweise [AB] drückt aus, dass es sich um eine Teilmenge der Geraden AB handelt, die durch die Punkte A und B begrenzt wird.

Die Strecke [AB] lässt sich mit Hilfe der Zwischen-Relation („… liegt zwischen … und …“) definieren: [AB] enthält alle Punkte der Geraden AB, die zwischen A und B liegen, sowie die Punkte A und B.

Unter der Länge der Strecke [AB] versteht man die Entfernung (den Abstand) der Punkte A und B. Diese Streckenlänge wird oft mit $\overline{AB}$, gelegentlich auch mit | AB | bezeichnet.

Zur Messung von Streckenlängen siehe Entfernungsmessung.

In der analytischen Geometrie entspricht die Strecke [AB] der Menge aller Punkte X, deren Ortsvektor $\vec{X}$ gegeben ist durch

$\vec{X} = \vec{A} + \lambda (\vec{B} - \vec{A})$ mit $0 \le \lambda \le 1$.

Dabei sind $\vec{A}$ und $\vec{B}$ die Ortsvektoren der Endpunkte A und B. λ ist der (reelle) Parameter dieser Parametergleichung.

Definition

Ist $V\,\!$ ein Vektorraum über $\mathbb{R}$ oder $\mathbb{C}$ und $L\,\!$ eine Teilmenge von $V\,\!$, so ist $L\,\!$ eine Strecke genau dann, wenn $L\,\!$ als $L = \{ \mathbf{u}+t\mathbf{v} \mid t\in[0,1]\}$ parametrisiert werden kann, wobei $\mathbf{u}, \mathbf{v} \in V\,\!$ zwei Vektoren sind und $\mathbf{v} \neq \mathbf{0}$ gelten muss. Dabei sind die Vektoren $\mathbf{u}$ und $\mathbf{u+v}$ die Endpunkte der Strecke $L.\,\!$

Manchmal unterscheidet man zwischen offenen und abgeschlossenen Strecken. Dabei wird die abgeschlossene Strecke wie oben definiert. Eine offene Strecke ist eine Teilmenge $L\,\!$, die als $L = \{ \mathbf{u}+t\mathbf{v} \mid t\in(0,1)\}$ parametrisiert werden kann, wobei wie oben $\mathbf{u}, \mathbf{v} \in V\,\!$ zwei Vektoren mit $\mathbf{v} \neq \mathbf{0}$ sind.

Eine alternative, äquivalente Definition ist wie folgt: Eine abgeschlossene Strecke ist die konvexe Hülle zweier verschiedener Punkte.

Eigenschaften

• Eine Strecke ist eine zusammenhängende, nicht leere Menge.
• Wenn V ein topologischer Vektorraum ist, ist die geschlossene Strecke eine abgeschlossene Menge in V. Eine offene Strecke ist jedoch eine offene Menge in V, genau dann, wenn V eindimensional ist.
• Allgemeiner kann der Begriff der Strecke in der Ordnungsgeometrie definiert werden.

Besondere Formen

• Kante - wenn die beiden Endpunkte die aneinander benachbarten Scheitelpunkte eines Vielecks sind
• Diagonale - wenn die beiden Endpunkte die aneinander nicht benachbarten Scheitelpunkte eines Vielecks sind
• Sehne - wenn die beiden Endpunkte auf einer Kurve, wie z.B. einem Kreis, liegen

Siehe auch: Geordnete Geometrie

Literatur

• H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S.10
• David Hilbert: Grundlagen der Geometrie. Teubner, Leipzig 1903, S.4

Weblinks

• Eric W. Weisstein: Line Segment. In: MathWorld. (englisch)
• Strecke auf PlanetMath (englisch)