Céa-Lemma

Das Céa-Lemma, oft auch Lemma von Céa oder Céas Lemma genannt, ist ein mathematischer Satz aus der Funktionalanalysis. Es ist grundlegend für die Fehlerschätzung von Finite-Elemente-Näherungen von elliptischen partiellen Differentialgleichungen. Das Lemma trägt den Namen zu Ehren des französischen Mathematikers Jean Céa^[1], der es in seiner Dissertation 1964 bewies.

Formulierung

Voraussetzungen

Sei V ein reeller Hilbertraum mit der Norm $\|\cdot\|$. Sei $a:V\times V\to \mathbb R$ eine Bilinearform, die

• beschränkt (äquivalent dazu stetig), d. h. $|a(v, w)| \le C \|v\|\,\|w\|$ für eine Konstante C > 0 und alle $v, w \in V$

• und koerzitiv (häufig auch stark positiv, V-elliptisch), d. h. $a(v, v) \ge \alpha \|v\|^2$ für eine Konstante α > 0 und alle $v \in V$

ist. Sei weiter $L:V\to \mathbb R$ ein beschränkter linearer Operator.

Problemstellung

Betrachte das Problem, ein $u \in V$ mit

$a(u, v)=L(v)\,$ für alle $v \in V$

zu finden. Betrachte nun das gleiche Problem in einem Unterraum $V_h \sub V$, d.h. es ist ein $u_h \in V_h$ zu finden mit

$a(u_h, v)=L(v)\,$ für alle $v \in V_h$.

Nach dem Lemma von Lax-Milgram gibt es für beide Probleme eine eindeutige Lösung.

Aussage des Lemmas

Sind die obigen Voraussetzungen erfüllt, dann besagt das Céa-Lemma:

$\|u-u_h\|\le \frac{C}{\alpha} \inf_{v_h \in V_h} \left(\|u-v_h\|\right)$.

Dies bedeutet, dass die Approximation der Lösung u_h aus dem Unterraum V_h nur um die Konstante $\tfrac{C}{\alpha}$ schlechter ist als die beste Approximation für u im Raum V_h, sie ist quasi-optimal.

Bemerkungen

Mit einer symmetrischen Bilinearform verkleinert sich die Konstante auf $\textstyle \sqrt{C/\alpha}$^[1], der Beweis ist weiter unten angegeben.

Das Céa-Lemma gilt auch für komplexe Hilberträume, indem eine Sesquilinearform $a(\cdot, \cdot)$ statt der Bilinearform verwendet wird. Die Koerzivität wird dann zu $|a(v, v)| \ge \alpha \|v\|^2$ für alle $v \in V$ (man beachte den Betrag um a(v,v)).

Die Approximationsgüte des Ansatzraums V_h bestimmt den Approximationsfehler $\|u-u_h\|$ stark.

Sonderfall: Symmetrische Bilinearform

Die Energienorm

In vielen Anwendungen ist die Bilinearform a symmetrisch, also a(v,w) = a(w,v) für alle v,w in V. Mit den Voraussetzungen des Céa-Lemmas ergibt sich, dass a ein Skalarprodukt von V ist. Die implizierte Norm $\|v\|_a=\sqrt{a(v, v)}$ wird Energienorm genannt, weil sie in vielen physikalischen Problemen eine Energie darstellt. Diese Norm ist äquivalent zur Norm $\|\cdot\|$ des Vektorraums V.

Das Céa-Lemma in der Energienorm

Die Unterraum-Lösung u_h ist eine Projektion von u auf den Unterraum V_h bezüglich des Skalarprodukts a.

Aus der Galerkin-Orthogonalität von u − u_h mit V_h und der Cauchy-Schwarzsche Ungleichung ergibt sich

$\|u-u_h\|_a^2 = a(u-u_h,u-u_h) = a(u-u_h,u-v) \le \|u-u_h\|_a \cdot \|u-v\|_a$ für alle v in V_h.

Somit lautet das Céa-Lemma in der Energienorm:

$\|u-u_h\|_a\le \|u-v\|_a$ für alle v in V_h.

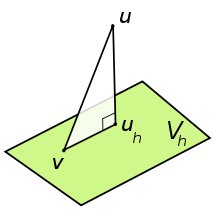
Man beachte, dass die Konstante $\tfrac{C}{\alpha}$ auf der rechten Seite verschwunden ist.

Das bedeutet, dass die Unterraum-Lösung u_h die beste Approximation der Lösung u bezüglich der Energienorm ist. Geometrisch lässt sich u_h als Projektion bezüglich a von u auf den Unterraum V_h interpretieren.

Folgerungen

Damit lässt sich die schärfere Schranke für symmetrische Bilinearformen für die gewöhnliche Norm $\| \cdot \|$ des Vektorraums V zeigen. Aus

$\alpha \|u-u_h\|^2 \le a(u-u_h,u-u_h) = \|u-u_h\|_a^2 \le \|u - v\|_a^2 \le C \|u-v\|^2$ für alle v in V_h

folgt

$\|u-u_h\| \le \sqrt{\frac{C}{\alpha}} \|u-v\|$ für alle v in V_h.

Beweis

Der Beweis ist nicht lang und führt die Notwendigkeit der Voraussetzungen vor Augen.

Galerkin-Orthogonalität

Die in der Problemstellung gegebenen Gleichung a(u,v) = L(v) für alle $v \in V$ und a(u_h,v) = L(v) für alle $v \in V_h$ werden voneinander abgezogen, was wegen $V_h \sub V$ möglich ist. Die resultierende Gleichung lautet a(u − u_h,v) = 0 für alle $v \in V_h$ und wird Galerkin-Orthogonalität genannt.

Abschätzung

Die Bilinearform a ist koerziv

$\alpha \|u-u_h\|^2 \le a(u-u_h,u-u_h)$

Addition von 0, sei $v_h \in V_h$

= a(u − u_h,u − v_h + v_h − u_h)

Mit Bilinearität von a

= a(u − u_h,u − v_h) + a(u − u_h,v_h − u_h)

Der zweite Term ist 0 wegen der Galerkin-Orthogonalität, da $v := v_h - u_h \in V_h$

= a(u − u_h,u − v_h)

Die Bilinearform ist a stetig

$\le \|u-u_h\| \|u-v_h\|$

Die Gleichung kann durch $\|u-u_h\|$ geteilt werden. Da v_h beliebig aus V_h gewählt ist kann auch das Infimum gewählt werden, wodurch wir die Aussage erhalten.

Literatur

• D. Braess: Finite Elemente - Theorie, schnelle Löser und Anwendungen in der Elastizitätstheorie. 4. Auflage. Springer, 2007, ISBN 978-3-540-72449-0 (Kapitel II §4.2 und Kapitel III §1.1).

• Jean Céa: Approximation variationnelle des problèmes aux limites. 14, Nr. 2, 1964, S. 345–444 (Original-Arbeit von J. Céa, PDF, 5 MB).

Einzelnachweise

1. ↑ ^{a b} E. Emmrich: Gewöhnliche und Operator-Differentialgleichungen - Eine integrierte Einführung in Randwertprobleme und Evolutionsgleichungen für Studierende. 1.Auflage. Vieweg+Teubner, 2004, ISBN 978-3-528-03213-5, Seite 112