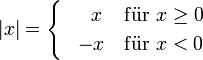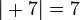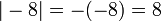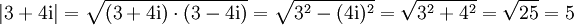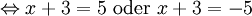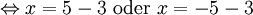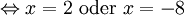- Absolute Zahl
-
In der Mathematik ordnet die Betragsfunktion einer reellen oder komplexen Zahl ihren Abstand zur Null zu. Dieser sogenannte absolute Betrag, Absolutwert oder auch schlicht Betrag ist immer eine nichtnegative, reelle Zahl. Der Betrag einer Zahl x wird meist mit | x | , seltener mit
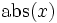 bezeichnet.
bezeichnet.Inhaltsverzeichnis
Reelle Betragsfunktion
Den absoluten Betrag einer reellen Zahl erhält man durch Weglassen des Vorzeichens. Auf der Zahlengerade bedeutet der Betrag den Abstand der gegebenen Zahl von null.
Für eine reelle Zahl x gilt:
Komplexe Betragsfunktion
Für eine komplexe Zahl
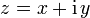 definiert man
definiert man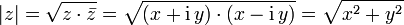 ,
,
wobei
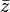 die komplex Konjugierte von z bezeichnet. Ist z reell, stimmt diese Definition mit der oberen überein.
die komplex Konjugierte von z bezeichnet. Ist z reell, stimmt diese Definition mit der oberen überein.Veranschaulicht man die komplexen Zahlen mithilfe der gaußschen Zahlenebene, so entspricht diese Definition nach dem Satz des Pythagoras dem Abstand der Zahl z von null.
Eigenschaften
- Die reelle Betragsfunktion
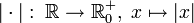 ist überall stetig, jedoch an der Stelle 0 nicht differenzierbar. Sie ist aber schwach differenzierbar und ihre schwache Ableitung stimmt fast überall mit der Signumfunktion überein.
ist überall stetig, jedoch an der Stelle 0 nicht differenzierbar. Sie ist aber schwach differenzierbar und ihre schwache Ableitung stimmt fast überall mit der Signumfunktion überein. - Die komplexe Betragsfunktion
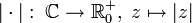 ist überall stetig und nirgends differenzierbar, da die Cauchy-Riemann-Differentialgleichungen nicht erfüllt sind.
ist überall stetig und nirgends differenzierbar, da die Cauchy-Riemann-Differentialgleichungen nicht erfüllt sind. - Definitionsbereich: Die Betragsfunktion ist auf ganz
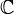 definiert.
definiert. - Die einzige Nullstelle ist |0| = 0.
- Für alle x gilt:
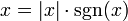
wobei sgn(x) die Signumfunktion bezeichnet.
Beispiele
Gleichung mit Absolutbetrag: Gesucht sind alle Zahlen
 , welche die Gleichung
, welche die Gleichung 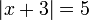 erfüllen.
erfüllen.Man rechnet wie folgt:
Die Gleichung besitzt also genau zwei Lösungen für x, nämlich 2 und -8.
Betrag und Metrik
Über den Betrag kann man eine Abstandsfunktion (Metrik) definieren: Der Abstand d(x,y) zweier Zahlen x und y ist der Betrag ihrer Differenz | x − y | .
Ist der Betrag nichtarchimedisch (siehe unten), dann ist die erzeugte Metrik eine Ultrametrik.
Verallgemeinerung: Betrag und Bewertung
Verallgemeinert spricht man von einem Betrag, wenn eine Funktion |·| von einem Körper K in die reellen Zahlen folgende Eigenschaften erfüllt:
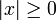 für alle x und | x | = 0 genau dann, wenn x = 0.
für alle x und | x | = 0 genau dann, wenn x = 0.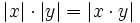 für alle x,y
für alle x,y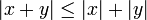 (die Dreiecksungleichung)
(die Dreiecksungleichung)
Gilt zudem
- 4.
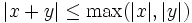
so spricht man von einem ultrametrischen oder nichtarchimedischen, andernfalls von einem archimedischen Betrag. Die oben genannte Betragsfunktion auf den reellen bzw. komplexen Zahlen ist archimedisch. Da 3. aus 4. folgt, nennt man 4. auch die verschärfte Dreiecksungleichung. Nichtarchimedische Beträge spielen eine wichtige Rolle in der Theorie der p-adischen Zahlen.
Hat man einen nichtarchimedischen Betrag |·|, und wählt eine reelle Zahl b > 1, dann hat die Funktion
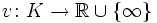 mit
mit
v(x) = − logb | x | für | x | > 0 und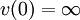 folgende Eigenschaften:
folgende Eigenschaften: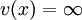 genau dann, wenn x = 0.
genau dann, wenn x = 0.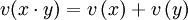 für alle x,y
für alle x,y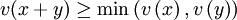
Eine Funktion
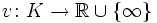 mit diesen drei Eigenschaften nennt man eine Bewertung auf K.
mit diesen drei Eigenschaften nennt man eine Bewertung auf K.Umgekehrt kann man einer Bewertung 'v' einen nichtarchimedischen Betrag zuordnen, indem man für eine reelle Zahl b > 1 setzt: | x | = b − v(x).
Weitere Verallgemeinerungen
Der Absolutbetrag ist eine spezielle Norm; den Begriff Norm kann man als eine Verallgemeinerung des Absolutbetrags verstehen.
Eine Abschwächung der Axiome für den Betrag führt auf den Begriff des Pseudobetrags.
Weblinks
- Eric W. Weisstein: Absolute Value auf MathWorld (englisch)
Wikimedia Foundation.