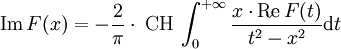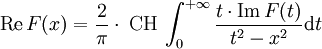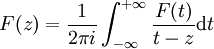- Kramers-Kronig-Relation
-
Die Kramers-Kronig-Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real- und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert-Transformation dar.
Inhaltsverzeichnis
Mathematische Formulierung
Sei
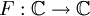 eine meromorphe Funktion, deren Polstellen in der unteren Halbebene liegen. Dieser Forderung an die Lage der Polstellen entspricht physikalisch das sog. Kausalitätspostulat. Ferner seien
eine meromorphe Funktion, deren Polstellen in der unteren Halbebene liegen. Dieser Forderung an die Lage der Polstellen entspricht physikalisch das sog. Kausalitätspostulat. Ferner seien 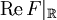 bzw.
bzw. 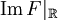 Real- und Imaginärteil der Funktion F. Es sei vorausgesetzt, dass diese beiden Funktionen gerade bzw. ungerade sind. (Das bedeutet, dass F durch Fourierintegration nicht aus einer beliebigen komplexen, sondern aus einer reellen Funktion gebildet werden kann.) In der Physik betrachtet man oft statt F die Funktion F/i, wodurch sich die Voraussetzungen bzgl. gerade und ungerade vertauschen. Schließlich sei
Real- und Imaginärteil der Funktion F. Es sei vorausgesetzt, dass diese beiden Funktionen gerade bzw. ungerade sind. (Das bedeutet, dass F durch Fourierintegration nicht aus einer beliebigen komplexen, sondern aus einer reellen Funktion gebildet werden kann.) In der Physik betrachtet man oft statt F die Funktion F/i, wodurch sich die Voraussetzungen bzgl. gerade und ungerade vertauschen. Schließlich sei 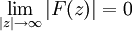 . Dann gelten für
. Dann gelten für 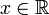 die folgenden, als Kramers-Kronig-Beziehungen bezeichnete Gleichungen:
die folgenden, als Kramers-Kronig-Beziehungen bezeichnete Gleichungen:CH bezeichnet den Cauchyschen Hauptwert des auftretenden Integrals.
Real- und Imaginärteil der Funktion F bedingen sich also gegenseitig, und zwar durch Integration, was vor allem in der Optik und der allgemeinen Systemtheorie (z. B. wenn F mit einer Suszeptibilität des Systems identisch ist, siehe Kausalität) vielfältige Anwendungen hat. Anwendungen finden sich aber auch in der Hochenergie-Physik ("Dispersionsrelationen" der S-Matrix).
Motivation (Ein Randwertproblem)
Auf der reellen Achse
 sei eine stetige reelle Funktion
sei eine stetige reelle Funktion 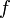 vorgegeben, die analog zu
vorgegeben, die analog zu 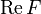 als gerade vorausgesetzt werden soll. Dazu soll eine in der ganzen oberen Halbebene holomorphe komplexe(!) Funktion
als gerade vorausgesetzt werden soll. Dazu soll eine in der ganzen oberen Halbebene holomorphe komplexe(!) Funktion 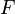 so konstruiert werden, dass
so konstruiert werden, dass 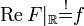 gilt.
gilt.Es soll also ein Randwertproblem gelöst werden, wobei im Innern des betrachteten Gebietes
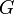 , d.h. oberhalb von
, d.h. oberhalb von  , wegen der Holomorphie-Bedingung die Cauchy-Riemannschen Differentialgleichungen erfüllt werden müssen und auf dem Rand,
, wegen der Holomorphie-Bedingung die Cauchy-Riemannschen Differentialgleichungen erfüllt werden müssen und auf dem Rand, 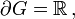 eine stetige reelle Funktion, f, vorgegeben ist, die dort angenommen werden soll.
eine stetige reelle Funktion, f, vorgegeben ist, die dort angenommen werden soll.Eine holomorphe Funktion kann nach dem Residuensatz dargestellt werden als:
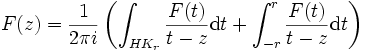 ,
,
wobei HKr(0) den (positiv orientierten) Halbkreis in der oberen Halbebene mit Zentrum 0 und Radius r > 0 bezeichnet. Fällt nun F im Unendlichen schnell genug ab, so reduziert sich im Grenzübergang
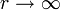 die Darstellung zu einem Integral über der reellen Achse, also:
die Darstellung zu einem Integral über der reellen Achse, also:Im Falle
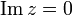 , und weil
, und weil 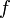 bzw.
bzw. 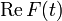 eine gerade Funktion sein soll, ergibt sich schließlich
eine gerade Funktion sein soll, ergibt sich schließlich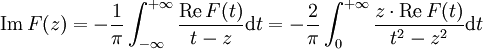 ,
,
wobei das auftretende Integral als Cauchyscher Hauptwert zu interpretieren ist (Singularität für t = z) und mit der Hilbert-Transformation von f übereinstimmt. Der Residuensatz wird hierbei auf den Integrationsweg
![[-r,z-\varepsilon] \cdot HK_\varepsilon(z) \cdot [z+\varepsilon, r] \cdot HK_r(0)](/pictures/dewiki/49/13b6a55e8e06de407f06464c4aefdb61.png) angewendet. Diese Gleichung entspricht der einen Kramers-Kronig-Beziehung.
angewendet. Diese Gleichung entspricht der einen Kramers-Kronig-Beziehung.Man braucht jetzt zur Lösung des Randwertproblems nur die Beziehung
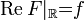 einzusetzen.
einzusetzen.Für ungerade Funktionen f verfährt man analog und erhält die andere Kramers-Kronig-Beziehung. Eine beliebige Funktion kann immer durch die Vorschrift
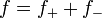 , mit
, mit 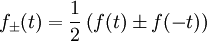 , in einen geraden bzw. ungeraden Anteil zerlegt werden.
, in einen geraden bzw. ungeraden Anteil zerlegt werden.Anwendungen
Die Kramers-Kronig-Beziehungen finden dort Anwendung, wo eine reelle gerade Funktion zu einer holomorphen Funktion ergänzt werden soll, was meistens der Vereinfachung der auftretenden Rechnungen dient, insbesondere bei Wellenfunktionen, also hauptsächlich in der Signalverarbeitung und in der Optik, aber auch in der Statistischen Physik im Zusammenhang mit dem Fluktuations-Dissipations-Theorem). Physikalisch wird dieses Instrument verwendet in Form einer Dispersions-Relation, die die elektromagnetische Absorption mit der Dispersion und damit mit der Brechzahl in Beziehung bringt.
Dadurch lässt sich die Kreisfrequenz-abhängige Absorption als eine Funktion der Kreisfrequenz-abhängigen Permittivität (Dielektrizitätskonstante) ε(ω) ausdrücken:
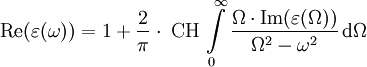
Eine alternative Betrachtungsweise ergibt sich mit dem Absorptionskoeffizienten α, der Brechzahl n und der Lichtgeschwindigkeit c:
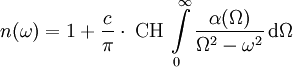
Dadurch lässt sich vor allem in der nichtlinearen Optik aus einer einfachen Absorptionsmessung die komplexe Form der Brechzahl ableiten.
Literatur
- Mansoor Sheik-Bahae: Nonlinear Optics Basics. Kramers-Kronig Relations in Nonlinear Optics, in: Robert D. Guenther (Hrsg.): Encyclopedia of Modern Optics, Academic Press, Amsterdam 2005, ISBN 0-12-227600-0
Wikimedia Foundation.