Irrationale Rotationsalgebra

Die irrationalen Rotationsalgebren werden im mathematischen Teilgebiet der Funktionalanalysis betrachtet. Es handelt sich um eine Klasse von C*-Algebren, die sich aus der C*-Algebra der stetigen Funktionen auf dem Einheitskreis zusammen mit einer Rotation dieses Einheitskreises um einen irrationalen Winkel ergeben.

Konstruktion

V dreht den Definitionsbereich von Funktionen $\mathbb{T}\to \C$

Im Folgenden sei θ eine fest gewählte irrationale Zahl. Wir betrachten den Hilbertraum L²$(\R/\Z)$, wobei wie üblich $\R/\Z$ mittels $t\mapsto e^{2\pi i t}$ mit dem Einheitskreis $\mathbb{T}=\{z\in \C: |z|=1\}$ identifiziert wird, und darauf die beiden wie folgt definierten unitären Operatoren U und V:

$Uf \,:=\, zf$, wobei z(t) = e^2πit

$Vf(t) \,:=\, f(t-\theta)$

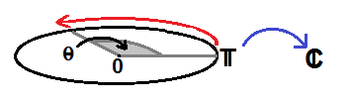
U ist ein Multiplikationsoperator und V rotiert eine Funktion um den Winkel θ.

Die von U und V erzeugte C*-Algebra $C^*(U,V)\subset B(L^2(\mathbb{T}))$ heißt daher die irrationale Rotationsalgebra zum Winkel θ und wird mit A_θ bezeichnet.^{[D 1]}

Eigenschaften

• Leicht bestätigt man UV = e^2πiθVU, in der Tat ist UVf(t) = U(Vf)(t) = z(t)Vf(t) = z(t)f(t − θ) = e^2πiθz(t − θ)f(t − θ) = e^2πiθ(zf)(t − θ) = e^2πiθ(Uf)(t − θ) = e^2πiθVUf(t).

• Die irrationale Rotationsalgebra hat folgende universelle Eigenschaft: Ist A eine C*-Algebra, die von zwei unitären Operatoren $\tilde{U}$ und $\tilde{V}$ erzeugt wird, die die Relation $\tilde{U}\tilde{V}=e^{2\pi i \theta}\tilde{V}\tilde{U}$ erfüllen, so gibt es genau einen *-Isomorphismus $A_\theta\rightarrow A$ mit $U\mapsto \tilde{U}$ und $V\mapsto \tilde{V}$.^{[D 2]}

• A_θ ist einfach, das heißt die Algebra enthält keine zweiseitigen *-Ideale außer {0} und sich selbst.

• Es gibt eine eindeutige Spur $\tau:A_\theta\rightarrow \C$, das heißt, es gibt genau ein lineares Funktional $\tau:A_\theta\rightarrow \C$ mit $\tau(a^*a)\ge 0$ für alle $a\in A_\theta$, τ(ab) = τ(ba) für alle $a,b \in A_\theta$ und τ(I) = 1, wobei I das Einselement in A_θ sei. ^{[D 3]}

• Die Gruppe der invertierbaren Elemente liegt dicht in A_θ.^[1]

• Die irrationalen Rotationsalgebren sind nuklear.

Alternative Konstruktion

Hier wird eine alternative Konstruktion der irrationalen Rotationsalgebra auf dem Folgenraum $\ell^2 = \ell^2(\Z)$ mit der Orthonormalbasis $(e_n)_{n_\in \Z}$ vorgestellt. Man definiere die unitären Operatoren $U,V\in B(\ell^2)$ durch:

$Ue_n \,=\, e_{n+1}$ (zweiseitiger Shift),

$Ve_n \,=\, e^{-2\pi i n \theta}e_n$ (unendliche Diagonalmatrix).

Dann bestätigt man leicht UVe_n = e ^{− 2πinθ}e_{n + 1} = e^2πiθVUe_n, woraus UV = e^2πiθVU folgt. Wegen der oben erwähnten universellen Eigenschaft der irrationalen Rotationsalgebra erhält man daraus $A_\theta \cong C^*(U,V) \subset B(\ell^2)$.

K-Theorie

Nach einem Satz von Marc Rieffel ^[2] gibt es zu jedem $\alpha\in (\Z+\theta \Z)\cap [0,1]$ eine Projektion $P\in A_\theta$ mit τ(P) = α, wobei τ die eindeutige Spur auf A_θ sei.

Da $(\Z+\theta \Z,(\Z+\theta \Z)\cap \R^+, (\Z+\theta \Z)\cap [0,1])$ eine unperforierte, skalierte, kommutative Gruppe mit der Rieszschen Zerlegungseigenschaft ist (für diese Begriffe siehe Geordnete abelsche Gruppe), gibt es nach dem Satz von Effros-Handelman-Shen bis auf Isomorphie genau eine AF-C*-Algebra $\mathcal{A}_\theta$, die diese Gruppe als K₀-Gruppe hat, und es liegt nahe die C*-Algebra A_θ, die selbst keine AF-Algebra ist, mit $\mathcal{A}_\theta$ in Verbindung zu bringen. Tatsächlich konnten M. Pimsner und D. Voiculescu eine Einbettung $A_\theta \rightarrow \mathcal{A}_\theta$ konstruieren^[3]. Daraus folgt zunächst $K_0(A_\theta) \cong \Z + \theta\Z$ und dann ^{[D 4]}:

• Zwei irrationale Rotationsalgebren A_θ und A_η sind genau dann isomorph, wenn $\eta = \pm\theta \,\mathrm{mod}\, \Z$ ist.

Verschränktes Produkt

Die irrationale Rotationsalgebra ist der Prototyp des verschränkten Produktes eines C*-dynamischen Systems. Ist $\alpha\in \mathrm{Aut}(C(\mathbb{T}))$ durch $(\alpha(f))(t) \,:=\, f(t-\theta)$ definiert und ist $\sigma:\Z\rightarrow \mathrm{Aut}(C(\mathbb{T})),\, n\mapsto \alpha^n$, so ist $(C(\mathbb{T}),\Z,\sigma)$ ein C*-dynamisches System und es ist $A_\theta \cong C(\mathbb{T})\ltimes_\sigma \Z$.^{[D 5]}

Einzelnachweise

1. ↑ I. Putnam: The invertibles are dense in the irrational rotation C*-algebras, J. reine angewandte Mathematik, Band 140 (1990), Seiten 160-166
2. ↑ M. A. Rieffel: C*-algebras associated with irrational rotations, Pacific J. Math., Band 93 (1981), Seiten 415-429
3. ↑ M. Pimsner, D. Voiculescu: Imbedding the irrational rotation algebra into an AF algebra, Journal of Operator Theory, Band 4 (1980), Seiten 93-118

K. R. Davidson: C*-Algebras by Example, American Mathematical Society (1996), ISBN 0-821-80599-1:

1. ↑ Kapitel VI: Irrational Rotation Algebra
2. ↑ Theorem VI.1.4
3. ↑ Satz VI.1.3
4. ↑ Korollar VI.5.3
5. ↑ Beispiel VIII.1.1