Tripel-Graph-Grammatik

Als Tripel-Graph-Grammatik (engl. triple graph grammar, kurz: TGG) bezeichnet man eine spezielle Art von Graphgrammatik, die vor allem für bidirektionale Modell-zu-Modell-Transformationen verwendet wird. Besonderheit von Tripel-Graph-Grammatiken ist, dass ihre Produktionsregeln aus drei Teilgraphen bestehen, von denen zwei die beiden beteiligten Modelle/Graphen repräsentieren (Quell- und Zielgraph). Der dritte Teilgraph, der sogenannte Korrespondenzgraph, verbindet zusammengehörige Graphteile aus Quell- und Zielgraph und liegt damit sozusagen „zwischen“ den beiden anderen Graphen.

Grundsätze und Semantik

Abb. 1: Klassische Notation einer TGG-Regel

Eine TGG besteht aus mehreren TGG-Regeln, deren Graphen typisiert und attributiert sind. Jede dieser Produktionsregeln beschreibt eine Möglichkeit, wie zwei Graphen und der zugehörige Korrespondenzgraph simultan verändert werden können. Diese Regeln sind also Graphersetzungregeln, deren linke Seite eine Vorbedingung (Mustergraph) und deren rechte Seite eine mögliche Ersetzung (Ersetzungsgraph) dafür angibt. Zusätzlich beschreibt ein sogenanntes Axiom, von welcher Ausgangssituation der drei Graphen die verschiedenen Regeln aus angewendet werden; ein Axiom entspricht somit dem Startsymbol bei klassischen Grammatiken.

Die einzelnen Produktionsregeln einer TGG sind monoton. Das heißt, dass sämtliche Knoten des Mustergraphen („linke Seite“) auch im Ersetzungsgraphen („rechte Seite“) vorhanden sind. („Links“ und „rechts“ bezieht sich hier nicht auf die Position innerhalb der graphischen Repräsentation der Regel, sondern sind die übliche Bezeichnung bei Graphersetzungssystemen.) Das heißt, dass mit TGGs keine Lösch-Operationen definiert werden können, was allerdings in Bezug auf das übliche Anwendungsgebiet keinen wirklichen Nachteil darstellt. Außerdem sind monotone Regeln weniger komplex (auch in Bezug auf den notwendigen Graph-Parser).

Die Graphelemente des Mustergraphen (linke Seite) bezeichnet man auch als Kontextgraph. Neu zu erzeugende Graphelemente, also Elemente, die sich nur auf der rechten und nicht der linken Regelseite befinden, werden auch als produzierter Graph bezeichnet.

Jede TGG definiert damit eine Sprache von Graph-Tripeln. Diese Sprache enthält alle Graph-Tripel, die vom Axiom aus unter Anwendung der gegebenen TGG-Regeln erzeugbar sind.

Eine solche TGG kann auch benutzt werden, um ausgehend von einem bestehenden Instanz-Quellgraph S den fehlenden Zielgraph T zu erzeugen. Dazu wird versucht, eine Abfolge von Produktionsregeln zu finden, die auf der Quellseite den Instanz-Quellgraphen S erzeugt. Modifiziert man nun dazu jeweils die Korrespondenz- und Zielgraphen wie in den TGG-Regeln definiert, so erhält man als Ergebnis das Graph-Tripel, das entstanden wäre, wenn man anhand der Regeln alle drei Graphen simultan neu erzeugt hätte.

Anwendung auf Modelle

Das TGG-Konzept lässt sich von Graphen auf MOF-Modelle übertragen. TGG-Regeln beschreiben dann, wie konkrete Instanz-Modelle modifiziert werden können. Zunächst wird die linke Seite der TGG-Regel per Pattern Matching in den Instanz-Modellen gesucht. Kann die linke Seite gefunden werden (d.h. die Regel ist anwendbar), so beschreibt die rechte Seite der Regel, wie die Regel angewendet wird, also wie die Instanzmodelle an dieser Fundstelle geändert werden können.

Modelle enthalten Objekte und Links, die Instanzen von Klassen und Referenzen eines Metamodells sind. Die Knoten einer TGG-Regel sind daher über die Klassen, die Kanten über die Referenzen des Metamodells typisiert. Ein Knoten kann beim Pattern Matching nur auf solche Objekte abgebildet werden, deren Klassen seinem Typ entsprechen. Genauso kann eine Kante einer TGG-Regel nur auf solche Links abgebildet werden, deren Referenzen ihrem Typ entsprechen.

Die drei Spalten einer TGG-Regel (Quell-, Korrespondenz- und Zielgraph) werden auch Domänen genannt. Eine Domäne hat typischerweise ein zugehöriges Metamodell. Die TGG-Knoten und -Kanten in dieser Domäne sind dann über diese Metamodell typisiert.

Grafische Syntax

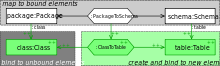
Die Regeln einer Tripel-Graph-Grammatik sind Graphen und werden klassischerweise in einer Art zweigeteiltem Objektdiagramm dargestellt, mit je einem Teil für die linke und rechte Regelseite (siehe Abb. 1). Die graphische Darstellung kann gegenüber einer textuellen einen intuitiveren Zugang ermöglichen.

Abb. 2: Kompakte Notation der TGG-Regel aus Abb. 1

Statt der klassischen Form der Darstellung (mit getrennter linker und rechter Seite) findet man häufiger eine kompakte Notation: Die gesamte Regel wird in nur einem Graphen dargestellt (siehe Abb. 2). Bei dieser kompakten Darstellung werden die Elemente des Mustergraphen (Kontext) meist schwarz und die des produzierten Graphen (also die Elemente, die nur auf der rechten Regelseite sind) grün markiert und mit bestimmten Markierungen (wie „<<create>>“ oder „++“) unterschieden.

Anwendungsszenarien

Grundsätzlich beschreibt eine Tripel-Graph-Grammatik, wie zwei Graphen parallel modifiziert werden können, um (gemäß der TGG) zueinander konsistent zu bleiben. Durch das Anwenden der Regeln können also zueinander konsistente Modelle erzeugt werden. In der Praxis wird dies allerdings selten angewendet; stattdessen werden TGGs für unterschiedliche Anwendungsszenarien interpretiert.

Vorwärts- und Rückwärtstransformation („Batch-Transformation“)

Abb. 3: Semantik der verschiedenen TGG-Regel-Teile bei einer Vorwärtstransformation

Im Anwendungsszenario Vorwärtstransformation soll ein existierendes Quellmodell in das neu zu erzeugende Zielmodell transformiert werden. Die grundsätzliche Idee besteht darin, eine Ableitungsreihenfolge gemäß dem TGG-Regelsatzes zu finden, die in der Quelldomäne das existierende Quellmodell erzeugen würde. Gemäß dieser Abfolge von Regeln kann dann das zugehörige Korrespondenz- und Zielmodell erzeugt werden. Das Finden dieser Ableitungsreihenfolge, das sogenannte Graphparsing, kann jedoch sehr aufwändig sein: Insbesondere wenn es mehrere Regeln gibt, die an derselben Stelle im Quellmodell passen, müssen gegebenenfalls alle diese Möglichkeiten ausprobiert werden.

Für den Anwendungsfall einer Vorwärtstransformation werden üblicherweise aus den Basisregeln Übersetzungsregeln abgeleitet bzw. die Basisregeln anders interpretiert: Da das Quellmodell bereits existiert, dürfen die Produktionen der Quelldomäne nicht ausgeführt werden. Die Knoten und Kanten im produzierten Graph der Quelldomäne werden stattdessen auf bereits existierende Quellmodellelemente abgebildet. So abgedeckte Modellelemente werden auch als gebunden bezeichnet. Dabei muss sichergestellt werden, dass jedes Element des Quellmodels nur genau einmal gebunden, also von einem produzierten Knoten oder einer produzierten Kante abgedeckt wird. Kontext-Knoten und -Kanten hingegen dürfen nur auf bereits gebundene Modellelemente abgebildet werden. Abb. 3 zeigt diese Richtlinien für eine Vorwärtstransformation. So wird sichergestellt, dass als Ergebnis der Transformation nur Modell-Tripel entstehen, die auch durch simultanes Erzeugen aller drei Modelle hätten entstehen können.

Eine Transformation ist nur dann vollständig, wenn alle Elemente des Quellgraphen gebunden sind, also von der Transformation bearbeitet wurden. Falls also noch Elemente des Quellgraphen ungebunden sind, aber keine Regel mehr anwendbar ist, ist die Transformation unvollständig. Falls zuvor an einer Stelle eine andere Regel anwendbar gewesen wäre, müsste nun zu dieser Stelle zurückgegangen werden und die andere Regel benutzt werden (Backtracking).

Die Richtung der Transformation ist umkehrbar, in dem lediglich die Bedeutung von Quell- und Zielmodell getauscht wird. Aus einer TGG sind also Vorwärts- und Rückwärtstransformationen ableitbar. Es müssen nicht manuell zwei verschiedene Transformationen für die beiden Richtungen spezifiziert werden.

Beispiel

Ein Beispiel für eine Modelltransformation im Kontext der Softwareentwicklung ist die objektrelationale Abbildung, bei der Objekte in einer relationalen Datenbank persistent abgelegt werden. Dazu werden für die Klassen, deren Objekte persistiert werden sollen, entsprechende Tabellen in der Datenbank angelegt.

Eine mögliche Abbildung von Klassen auf Tabellen ist, pro Vererbungshierarchie eine Tabelle anzulegen. Eine Basisklasse wird also in eine Tabelle übersetzt, alle von ihr abgeleiteten Klassen verwenden ebenfalls diese Tabelle der Basisklasse. Die in Abb. 2 gezeigte TGG-Regel stammt aus einem Regelsatz, der eine solche Abbildung definiert. Diese Regel beschreibt, dass jeder Basisklasse in der Domäne Klassen eine Tabelle in der Domäne Datenbank entspricht.

Abb. 4: Vorwärtstransformation von Klassen in ein Datenbankschema (animiert)

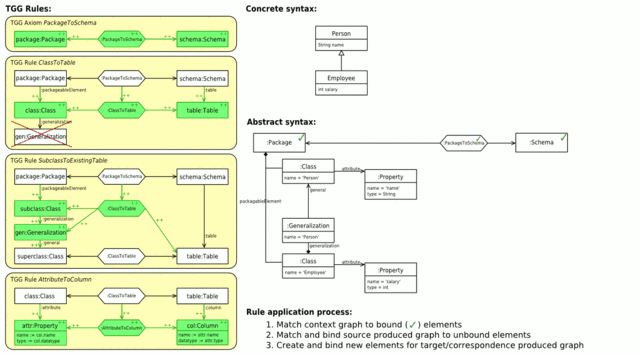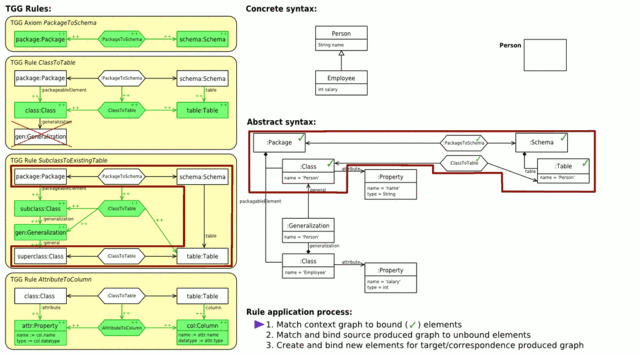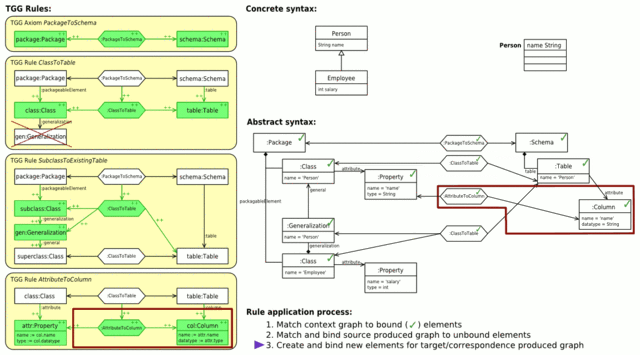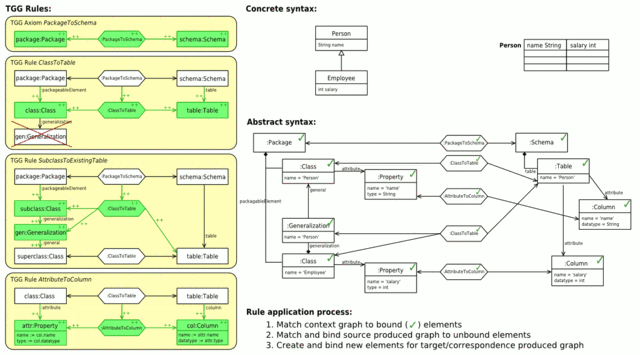
Abb. 4 zeigt links den gesamten TGG-Regelsatz für diese Abbildung. An oberster Stelle befindet sich das Axiom, dass einem Paket ein Datenbankschema zuordnet. Die nächste Regel ordnet einer Basisklasse eine Tabelle zu. Die negative Anwendungsbedingung verhindert, dass diese Regel auch für abgeleitete Klassen angewendet wird. Die dritte Regel ordnet dann abgeleitete Klassen der Tabelle ihrer Basisklasse zu. Dies funktioniert auch für mehrstufige Vererbung, da der Kontext der Regel auch von dem produzierten Teil derselben Regel gebildet werden kann. Die letzte Regel übersetzt schließlich Attribute einer Klasse in Spalten in der entsprechenden Tabelle der Klasse.

Rechts sieht man, wie in einer Vorwärtstransformation Schritt für Schritt durch Anwendung der verschiedenen TGG-Regeln das Zielmodell aus dem Quellmodell erstellt wird. In der Ausgangssituation sind dabei bereits die Wurzelelemente der drei Modelle (die Objekte :Package, :PackageToSchema, :Schema) durch das Axiom gebunden. Nun wird versucht, die verschiedenen TGG-Regeln anzuwenden. Jede TGG-Regel wird dabei in drei Schritten bearbeitet:

1. Zunächst wird versucht, per Pattern Matching zum Kontextgraphen der Regel passende Teile in Quell-, Ziel- und Korrespondenzmodell zu finden.
2. Wurde in Schritt 1 ein zum Kontextgraphen passender Teil gefunden, so wird anschließend ein zum produzierten Quellgraphen passender Teil im Quellmodell gesucht.

Wird ein passender Teil im Quellmodell gefunden, werden die entsprechenden Elemente als gebunden markiert und mit Schritt 3 fortgefahren. Kann kein Teil gefunden werden, so wird zu Schritt 1 zurückgegangen und ein anderes Pattern Matching für den Kontextgraphen gesucht.

1. Wurde in Schritt 2 ein Matching für den Kontext- und produzierten Quell-Teil der Regel gefunden, die Regel angewendet werden.

Dabei werden für den produzierten Korrespondenz- und Ziel-Teil der Regel Modellelemente erzeugt und gleichzeitig als gebunden markiert. Abschließend werden noch eventuell notwendige Attributwertzuweisungen durchgeführt.

Abb. 5: Pattern-Matching-Ablauf und Anwendung einer Regel (animiert)

Abb. 5 zeigt beispielhaft, wie das Pattern Matching und die Anwendung einer TGG-Regel zur Übersetzung von Attributen abläuft.

Synchronisation („inkrementelle Transformation“)

Mithilfe von Tripel-Graph-Grammatiken können nicht nur einmalige Modelltransformationen (Batch-Transformationen) durchgeführt werden. Durch den Korrespondenzgraph werden zusammengehörige Modellteile markiert, so dass auch nachträgliche Änderungen an einem der Modelle in das andere Modell übertragen werden können, ohne diese vollständig neu zu erzeugen („inkrementelle Transformation“).

Wird beispielsweise ein neues Modellelement hinzugefügt, braucht lediglich geprüft werden, ob durch diese Einfügung weitere Regeln anwendbar sind, um diese dann ausführen. Neben einer verbesserten Laufzeit hat dies den Vorteil, dass möglicherweise zwischenzeitlich ins Zielmodell eingefügte modellspezifische Informationen (also Informationen ohne Relevanz für die Modelltransformation) nicht verloren gehen.^[1]

Geschichte

Tripel-Graph-Grammatiken sind eine Erweiterung von Pair-Grammatiken. Sie wurden 1993 von Andy Schürr entwickelt und 1994 das erste Mal in der wissenschaftlichen Publikation „Specification of Graph Translators with Triple Graph Grammars“ veröffentlicht. Im Gegensatz dazu und zu EBNF-basierten Ansätzen erlauben sie auch Produktionen, die nicht mehr kontextfrei sind: Mithilfe des Korrespondenzgraphen kann explizit auf vorherige Regelanwendungen Bezug genommen werden („kontextsensitiv“).

Während sich in den ersten Jahren nach der Veröffentlichung die Bekanntheit von TGGs noch in Grenzen hielt, stieg um das Jahr 2000 die Anzahl wissenschaftlicher Publikationen zum Thema deutlich an. Die erste Veröffentlichung wurde bis zum Jahr 2011 von über 400 Publikationen zitiert.^[2]

Seit der Vorstellung von TGGs sind zahlreiche Änderungen und Ergänzungen für das Konzept vorgeschlagen worden. Es existiert eine Vielzahl an Systemen und Implementierungen, die auf TGGs oder Abwandlungen davon basieren.

Als Lösung für Modell-zu-Modell-Übersetzungen konkurriert es unter anderem mit dem QVT-Standard der Object Management Group. QVT-Relations, ein Teil der QVT-Spezifikation, hat allerdings große Ähnlichkeiten zu TGGs.

TGG-Tools

Programme für Modelltransformationen mit TGGs wurden bislang vor allem an Universitäten entwickelt. Es existieren mehrere Ansätze, die sich in Ausrichtung und verwendeter Technologie unterscheiden.

Name	Hersteller	Lizenz	Anmerkungen
TGG-Interpreter	Universität Paderborn	EPL (Open-Source)	Eclipse/EMF-basiert, TGG-Regeln werden zur Laufzeit interpretiert
MOFLON	TU Darmstadt	LGPL (Open-Source)	MOF-2.0-basiert
Fujaba	Universität Paderborn u.a.	LGPL (Open-Source)	Entwicklung des TGG-Teilprojekts eingestellt
IMPROVE	RWTH Aachen	?
MDELab, Plug-in MoTE	Hasso-Plattner-Institut	CPL (Open-Source)	Eclipse/EMF-basiert, TGGs werden zur Ausführung in Story-Diagramme übersetzt

Verwandte Ansätze

Andere deklarative Modelltransformationssprachen wie Tefkat oder MOF QVT-R haben Ähnlichkeiten zu TGGs. ATL als hybride Transformationssprache hat neben imperativen Anteilen ebenfalls deklarative Konstrukte.

Literatur

• A. Schürr: Specification of Graph Translators with Triple Graph Grammars. In: Proceedings of the 20th International Workshop on Graph-Theoretic Concepts in Computer Science. Lecture Notes In Computer Science. Vol. 903, 1994, doi:10.1007/3-540-59071-4_45 (PDF-Datei; 75 KB).
• A. Königs, A. Schürr: Tool Integration with Triple Graph Grammars - A Survey. In: Electronic Notes in Theoretical Computer Science. Vol. 148, 2006, S. 113–150, doi:10.1016/j.entcs.2005.12.015.
• H. Giese, R. Wagner: From model transformation to incremental bidirectional model synchronization. In: Software and Systems Modeling. Vol. 8, Nr. 1, 2009, S. 23–43, doi:10.1007/s10270-008-0089-9.
• J. Greenyer, E. Kindler: Comparing relational model transformation technologies: implementing Query/View/Transformation with Triple Graph Grammars. In: Software and Systems Modeling. Vol. 9, Nr. 1, 2010, S. 21–46, doi:10.1007/s10270-009-0121-8.

Einzelnachweise

1. ↑ J. Greenyer, S. Pook, J. Rieke: Preventing Information Loss in Incremental Model Synchronization by Reusing Elements. In: Modelling Foundations and Applications. Lecture Notes In Computer Science. Vol. 6698, 2011, S. 144–159, doi:10.1007/978-3-642-21470-7_11.
2. ↑ Zitationen der Publikation „Specification of Graph Translators with Triple Graph Grammars“. Google Scholar, abgerufen am 1. November 2011.