Ćuk-Wandler

Als Ćuk-Wandler (englisch Ćuk converter) bezeichnet man in der Elektronik eine diskrete elektronische Schaltung, die eine elektrische Gleichspannung in eine andere elektrische Gleichspannung transformieren kann. Der Betrag der Ausgangsspannung kann dabei sowohl kleiner als auch größer sein als die Höhe der ursprünglichen Eingangsspannung. Im Gegensatz zu dem SEPIC-Wandler weist die Ausgangspannung wie beim Inverswandler gegenüber der Eingangsspannung ein negatives Vorzeichen auf, die Ausgangsspannung ist invertiert. Aufgrund dieser Tatsache wird der Ćuk-Wandler zur Gruppe der invertierenden Gleichspannungswandler gezählt.

Die Bezeichnung Ćuk-Wandler ist auf den Namen dessen Erfinders Slobodan Ćuk zurückzuführen, der die Schaltungsidee 1976 zusammen mit Robert D. Middlebrook vorstellte^[1].

Aufbau und Motivation

Prinzipschaltbild des Ćuk-Wandlers mit einem Wechselschalter

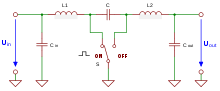
Der Ćuk-Wandler verwendet für die Spannungswandlung drei aktive Energiespeicher, zwei Spulen und einen Kondensator, welche mithilfe von Halbleiterschaltern kontinuierlich mit Energie geladen und entladen werden. Zusätzlich wird, wie bei jedem Spannungswandler, sowohl am Eingang, als auch am Ausgang ein Ladekondensator benötigt, um die Spannungswelligkeit zu reduzieren.

Bei gewöhnlichen Spannungswandlern wie dem Aufwärtswandler oder dem Abwärtswandler tritt entweder am Eingang, oder am Ausgang der Schaltung ein diskontinuierlicher Stromverlauf auf, welcher die jeweilige Spannungswelligkeit negativ beeinflusst. So muss bei Aufwärtswandler der Ausgangskondensator besonders groß sein, da der Wandler nur in der Ausschaltzeit des Schalters Strom an der Ausgang liefert. Beim Abwärtswandler hingegen muss wiederum auf den Eingangskondensator besonders Augenmerk gelegt werden, da hier der nur in der Einschaltzeit des Schalter Strom vom Eingang in die Schaltung fließt.

Genau diese negativen Eigenschaften treten bei der Ćuk-Wandler-Topologie nicht auf, da hier sowohl der Eingangsstrom, als auch der Ausgangsstrom kontinuierlich verlaufen. Somit können beide Ladekondensatoren deutlich kleiner ausfallen, ohne die Spannungswelligkeit zu verschlechtern.

Funktion

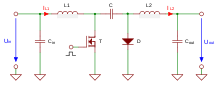Schaltbild einer praktischen Ausführung des Ćuk-Wandlers mit einem MOSFET. Um eine bessere Effizienz zu erreichen, kann die Diode ebenfalls als Transistor ausgeführt werden.

Wird der Transistor T eingeschaltet, so liegt die Induktivität L1 parallel zur Versorgungsspannung und der Strom I_L1 beginnt zu steigen. Nach dem Abschalten des Transistors fließt dieser Strom auf Grund der lenzschen Regel weiter, und lädt den Kondensator C über die Diode D. Der Strom in der Induktivität L1 nimmt dabei ab, die Spannung am Kondensator zu. Nach dem erneuten Einschalten des Transistors wird die Induktivität L1 nachgeladen und der Strom I_L1 steigt. Gleichzeitig beginnt nun ein negativer Strom I_L2 zu fließen, der ausgehend von Kondensator über die Induktivität L2 und über die Last (inklusive Ladekondensator) fließt, und dem Kondensator Energie entzieht. Am Ladekondensator des Ausgangs baut sich somit eine negative Spannung auf. Nach erneutem Abschalten des Transistors wird der Kondensator vom Strom I_L1 nachgeladen. Gleichzeitig fließt der, ebenfalls bedingt durch die lenzschen Regel, von Induktivität L2 hervorgerufene Strom I_L2 durch die Last und die Diode weiter.

Somit weist sowohl der Eingangsstrom, als auch der Ausgangsstrom, einen kontinuierlichen Verlauf auf.

Mathematische Beschreibung

Für die folgenden Überlegungen wird davon ausgegangen, dass alle Kondensatoren sehr groß sind und der Wandler bei konstantem Tastverhältnis eingeschwungen ist.

Der Strom in den beiden Induktivitäten schwankt kontinuierlich um zwei Werte. Der Mittelwert diese Ströme sind konstant und die Ladung am Kondenstor im Mittel ausgeglichen.

$\int_{t_0}^{t_1} i_{L1}\,\mathrm{d}t + \int_{t_1}^{t_2} i_{L2}\,\mathrm{d}t = 0$

Nimmt man weiter an, dass der Stromverlauf in der Induktivitäten dreieckförmig ist, können die Integrale vereinfacht werden.

$\overline{i_\mathrm{L1}} \cdot t_\mathrm{on} + \overline{i_\mathrm{L2}} \cdot t_\mathrm{off} = 0$

Ersetzt man die Zeiten durch das Tastverhältnis (d), erhält man folgenden Ausdruck.

$\dfrac{\overline{i_\mathrm{L2}}} {\overline{i_\mathrm{L1}}}= \dfrac{-d}{1-d}$

Die Spannung an einer Induktivität ergibt sich zu:

$u_\mathrm{L}\left(t\right) = -L \cdot \frac{\mathrm{d}i_L\left(t\right)}{\mathrm{d}t}$

Demnach müssen die Mittelwerte der Spannungen an den beiden Induktivitäten null ergeben.

Die Spannung an der Induktivität L1 ergibt sich somit zu:

$d \cdot U_\mathrm{in} + (1-d) \cdot (U_\mathrm{in} - U_\mathrm{C}) = 0$

$U_\mathrm{C} = \dfrac{U_\mathrm{in}}{1-d}$

Die Spannung an der Induktivität L2 ergibt sich zu:

$d \cdot (U_\mathrm{C}+U_\mathrm{out}) + (1-d) \cdot U_\mathrm{out} = 0$

$U_\mathrm{C} = -\dfrac{U_\mathrm{out}}{d}$

Durch gleichsetzen der beiden Gleichungen erhält man eine Gleichung, die die Ausgangsspannung des Ćuk-Wandlers in Abhängigkeit der Eingangsspannung und des Tastverhältnisses darstellt:

$U_\mathrm{out} = -U_\mathrm{in} \cdot \dfrac{d}{1-d}$

Ausführung

Der Ćuk-Wandler kann sowohl nicht isolierend als auch isolierend mittels Übertrager ausgeführt werden. Bei letzterem besteht zusätzlich die Möglichkeit die Ausgangsspannung um das Übertragungsverhältnis des Transformators zu erhöhen oder zu verringern.

Die beiden Induktivitäten können magnetisch gekoppelt werden, was die Spannungswelligkeit am Eingang und Ausgang verringert. Dabei verwenden die beiden Induktivitäten denselben Kern als magnetische Koppelung.

Siehe auch

• Sperrwandler
• Eintaktflusswandler
• Gegentaktflusswandler

Literatur

• M. H. Rashid: Power Electronics Handbook, Second Edition: Devices, Circuits and Applications (Engineering) 2. Auflage, Academic Press, Burlington, California, 2007, ISBN 978-0-12-088479-7.

Weblinks

• Grundlagen von Gleichspannungswandlern
• Dimensionierung des Ćuk-Wandlers

Einzelnachweise

1. ↑ R. D. Middlebrook, S. Ćuk: A general unified approach to modelling switching-converter power stages. In: Proceedings of the IEEE Power Electronics Specialists Conference, June 8 - 10, 1976, Cleveland, OH. 1976, S. 73–84 (Vorabdruck als PDF, abgerufen am 5. Juli 2010).