Deduktion

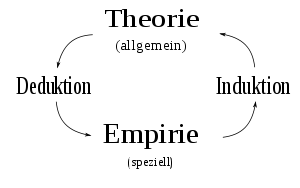
Die Deduktion (lat.: deductio, „Abführen, Fortführen, Ableitung“), auch deduktive Methode oder deduktiver Schluss, ist in der Philosophie und der Logik eine Schlussfolgerung von gegebenen Prämissen auf die logisch zwingenden Konsequenzen. Deduktion ist schon bei Aristoteles als Schluss vom Allgemeinen auf das Besondere verstanden worden und als Gegensatz zur Induktion, der Gewinnung von allgemeinen Erkenntnissen aus speziellen, und der Abduktion. Deduktion, Induktion und Empirie bilden die zentralen Pfeiler in der klassischen Wissenschaftstheorie, wobei die Theorie die Rolle des Allgemeinen und vorherzusagende (Deduktion) bzw. bereits beobachtete Tatsachen (Induktion) die Rolle des Speziellen spielt.

Der Gegensatz zwischen Deduktion und Induktion

Logik und formale Systeme

Innerhalb der modernen mathematischen Logik und allen formalen Systemen wird ein möglichst durchgehender Aufbau mit deduktiven Prinzipien angestrebt. Auch die Mathematik liegt weitgehend in deduktivem Aufbau vor und wird vorwiegend so gelehrt; d. h. ihre Ergebnisse werden aus Axiomensystemen formal abgeleitet. Deduktive Geschlossenheit ist ein wesentliches Merkmal formaler Beweise in der Mathematik (s. a. Beweis (Mathematik)) die mathematischen Verfahren der Vollständigen Induktion und der transfiniten Induktion sind entgegen ihres Namens deduktive Verfahren.

Der einfachste Fall der Anwendung der deduktiven Methode ist die Beseitigung einer Implikation mit Hilfe der Abtrennungsregel. Die logische Struktur dieser Regel ist die allgemeine Struktur eines Arguments, dass aus einer Menge von Prämissen nach einer Schlussregel auf eine Konklusion schließt:

p p → q ——— q (Prämisse 1) (Prämisse 2) (Konklusion)

Sind p und p → q (sprich: wenn p, dann q) wahre Aussagen, so ist auch q eine wahre Aussage.

Entscheidbarkeit

Es gibt logische Systeme, in denen Ausdrücke auftreten, die zwar mit den Hilfsmitteln dieses Systems formuliert werden können, in ihm aber nicht entscheidbar sind. Deduktive und reduktive Schlussweisen werden in ihrer einfachen Struktur nur selten angewandt. Das tatsächlich wissenschaftliche Ableiten ist ein komplexes System von deduktiven, reduktiven und heuristischen Verfahren.

Siehe auch: Entscheidbar

Wissenschaftstheorie

Die Auffassung, dass Deduktion und Induktion komplementäre Elemente der wissenschaftlichen Wahrheitsfindung sind, ist auch bestritten worden, am prominentesten von Karl Popper. Ihm zufolge handelt es sich bei der Induktion nicht um ein Beweisverfahren. Allgemeine Regeln werden in Poppers Falsifikationismus nicht nach bestimmten induktiven Regeln aus der Empirie hergeleitet, solche Regeln sind ihm zu Folge bestenfalls Heuristiken für das Finden allgemeiner Hypothesen. Alle Schlüsse, die in der Wissenschaft gezogen werden, sind für ihn daher rein deduktiv, auch Schlüsse vom Besonderen auf das Allgemeine: Diese erfolgen im modus tollens, beispielsweise wenn eine allgemeine Hypothese oder Theorie ausgehend von einer beobachteten Einzeltatsache falsifiziert werden (siehe auch indirekter Beweis).

In den Naturwissenschaften müssen durch Deduktion ermittelte Vorhersagen empirisch überprüfbar sein, um einen wissenschaftlichen Wert zu besitzen. Wenn die Beobachtungen nicht mit den Vorhersagen übereinstimmen, muss die Theorie angepasst oder verworfen werden.

Die deduktive Methode wird allgemein aber nicht für die einzige Methode der Gewinnung neuer wissenschaftlicher Erkenntnisse gehalten. Solch eine Methode muss stets von Prämissen ausgehen, die ihrerseits als wahr zu beweisen sind, hypothetisch als wahr vorausgesetzt werden oder axiomatisch als wahr gesetzt sind. Selbst wenn sich solche Prämissen wiederum aus anderen Prämissen deduktiv ableiten lassen, muss diese Beweiskette doch irgendwo beginnen (siehe: Infiniter Regress).

Die Wissenschaft muss zu Beweisverfahren greifen, die nicht-deduktiver Natur sind, denen also intensionale Beziehungen zugrunde liegen. Es handelt sich dabei also um empirische Verfahren, welche Erkenntnisse durch Beobachtung und Experimente gewinnen. Die logische Verarbeitung der Ergebnisse der Praxis zu wissenschaftlichen Aussagen oder gar Gesetzen geschieht mit der reduktiven Methode.

Psychologie

Neben Logik, Philosophie und Linguistik beschäftigt sich auch die Denkpsychologie für die menschlichen Kompetenz und Inkompetenz beim schlussfolgernden Denken.^[1] Als wichtigste Theorien sind zu nennen:

• die Theorie der mentalen Modelle von Philip Johnson-Laird (1983),
• die Theorie der mentalen Logik von Jean Piaget (1958), Rips (1994), Ford (1995) und anderen sowie
• die Informationsgewinn-Theorie von Oaksford und Chater (1994).

Die Psychologie untersucht, warum und wie Menschen überhaupt schlussfolgern können, warum sie dabei Fehler machen und welche Fehler häufiger gemacht werden als andere. Um Inhaltseffekte auszuschließen, hat man sich dabei meist syllogistischer Aufgaben bedient. Es zeigte sich, dass Menschen sehr häufig nicht formal-logisch denken, sondern stattdessen, besonders unter Zeitdruck, Heuristiken benutzen. Dabei lassen sich systematische Fehler erkennen, die in der Fachliteratur als Bias (engl. für Vorurteil, Befangenheit, Tendenz) bezeichnet werden. So werden unlogische, aber vom Inhalt her glaubwürdige Schlussfolgerungen oft für wahr gehalten, ebenso logisch valide, aber unglaubwürdige Konklusionen irrtümlich für falsch (belief bias^[2]). Ebenfalls verbreitet ist die Tendenz, Schlussfolgerungen eher für wahr zu halten, die die eigenen Überzeugungen bestätigen (sog. confirmation bias). Umfangreiche Listen von kognitiven Biases finden sich unter List of cognitive biases und Category:Cognitive biases in der englischsprachige Wikipedia.

Siehe auch

• Axiomensystem; Axiomatisierung
• Deduktionstheorem
• Deduktive Argumentate
• Deduktiv-nomologisches Modell
• Fehlschluss
• Formales System

Weblinks

• Deduktion aus psychologischer Sicht, arbeitsblaetter.stangl-taller.at
• Deduktion naturwissenschaftlich, Ruprecht-Karls-Universität Heidelberg, www.uni-heidelberg.de
• Alan Baker: Non-Deductive Methods in Mathematics, in: Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)

 Wiktionary: Deduktion – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

1. ↑ P. Johnson-Laird und R. Byrne: Deduction. Psychology Press, Hove (GB) 1991. ISBN 0-86377-148-3.
2. ↑ Vgl. z.B. H. Markovits / G. Nantel: The belief-bias effect in the production and evaluation of logical conclusions, in: Memory and Cognition 17/1 (1989), 11–17.