Hypothesen

Als eine Hypothese (altgriechisch ὑπόθεσις (hypóthesis) – die Unterstellung, Voraussetzung, Grundlage) bezeichnet man eine Aussage, deren Gültigkeit bloß vermutet wird, die aber im Gegensatz zu einer Spekulation nicht nur anscheinend widerspruchsfrei ist und in Übereinstimmung mit dem allgemeinen Wissen steht, sondern auch begründet werden kann. Für Hypothesen ist es üblich, dass die Bedingungen angegeben werden, unter denen sie gültig sein sollen.

Empirische Wissenschaften

In den empirischen Wissenschaften haben Hypothesen den Status einer Annahme, die üblicherweise nach dem deduktiv-nomologischen Modell überprüft werden. Dabei werden beobachtete Daten auf die Hypothese angewendet und damit verglichen, ob die Ergebnisse mit den tatsächlich beobachteten Ereignissen übereinstimmen. Ist die Übereinstimmung gegeben, wurde die Hypothese bestätigt und die zugrunde liegende Theorie, die neben der Hypothese auch die Prämissen und die Versuchsanordnung beinhaltet, hat sich bewährt. Hypothesen, die keiner empirischen Überprüfung unterzogen werden können, gelten nicht als wissenschaftlich (siehe Falsifizierbarkeit).

Hypothesen dienen entweder der Erklärung schon bekannter Tatsachen oder als Prämissen allgemeiner empirischer Gesetzesaussagen. Da empirische Gesetze nur durch eine endliche Anzahl von Beobachtungen bestätigt werden können (siehe Induktion), können solche Aussagen nicht als endgültig bewiesen, sondern nur als bewährt betrachtet werden.

Werden Hypothesen als vorläufige Annahmen formuliert, um die möglichen Grundannahmen einer noch aufzustellenden Theorie zu überprüfen, spricht man von Arbeitshypothese.

Können mehrere Hypothesen ein Ereignis erklären, kann durch den Schluss auf die beste Erklärung eine Hypothese vor einer rivalisierenden Hypothese ausgezeichnet werden.

Logik

In einem logischen Gespräch ist eine Hypothese die Prämisse eines Arguments, deren Wahrheit zunächst ausgeklammert wird. Dabei wirken Hypothesen als Implikationen, die der Verteidigung einer These dienen. Formal:

A₁, . . . . , A_n $\Rightarrow A$

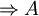
Ist die These (die Konsequenz A) unter Annahme der Hypothesen gültig, müssen die einzelnen Hypothesen überprüft werden.

Mathematik

In der Mathematik bezeichnet der Begriff Hypothese ursprünglich die unbewiesenen Grundlagen oder allgemeinen Prinzipien, aus denen die mathematischen Sätze abgeleitet werden. Da diese Prinzipien als Axiome verwendet werden, gilt für sie nicht das Kriterium der Wahrheit. Sie sind gesetzt. Die mit ihnen verbunden Schlussfolgerungen sind deduktiv.

Statistische Hypothesen

Bei der statistischen Hypothese, die mit einer bestimmten Wahrscheinlichkeit falsifiziert werden kann, wendet man statistische Tests an. Siehe auch: Statistik, Fehler 1. und 2. Art

Historische Aspekte

Platon

Platon behandelte das Thema der Hypothese mehrfach, so auch in seinem Dialog Phaidon (100 a):

„Ich lege meiner Untersuchung immer eine Behauptung zugrunde, die ich für besonders stark halte; und das von dem ich dann den Eindruck habe, dass es damit in Einklang steht, nenne ich wahr; was dagegen damit nicht in Einklang zu stehen scheint, nenne ich unwahr.“

Abduktion bei Charles S. Peirce

Charles S. Peirce bezeichnete den Schluss von einem Ereignis unter Annahme einer Regel auf einen Fall als eine Hypothese, die eine eigene Schlussweise neben Induktion und Deduktion darstellt. Sehe ich zum Beispiel Rauch und gehe von der Regel aus „Wo Rauch ist, ist auch Feuer“ komme ich zu dem Schluss „Dort ist Feuer“. Die Schlussweise der Hypothese ist logisch nicht eindeutig. (siehe auch Abduktion).

Arten von Hypothesen nach Poincaré

Der Philosoph und Wissenschaftler Henri Poincaré unterschied drei Arten von Hypothesen:

1. Natürliche Hypothesen. Dies sind Hypothesen ganz allgemeiner Art, die sich als Hintergrundwissen widerspiegeln. Beispiele sind die Existenz der Außenwelt und die prinzipielle Erkennbarkeit der Dinge. Natürliche Hypothesen können nur schwer aufgegeben werden, da sie für den Wissenschaftsbetrieb konstitutiv sind.
2. Indifferente Hypothesen. Diese Hypothesen funktionieren als Konventionen, da man für eine Theorie auch die gegenteilige Hypothese annehmen könnte und dies die Theorie lediglich verkomplizieren, nicht aber widerlegen würde.
3. Verallgemeinernde Hypothesen. Durch Erfahrung bestätigbar oder widerlegbar ist nur diese Art Hypothesen. Sie werden durch Induktionsschlüsse gewonnen.

Berühmte Hypothesen

Joint-Hypothese, Gaia-Hypothese, Savannen-Hypothese, Anatolien-Hypothese, Wobble-Hypothese, Kurgan-Hypothese, Frustrations-Aggressions-Hypothese, Balto-slawische Hypothese, Sapir-Whorf-Hypothese, Drei-Sektoren-Hypothese, Ein-Gen-ein-Enzym-Hypothese

Anschauliche Zitate

„Hypothesen, noch vibrierend von eigener In-Frage-Stellung, kommen selten bereits zum praktischen Beweis, zu dem der technischen, sozialen Veränderung, als gelingender. Sie bleiben im bloßen Versuch des bloßen Erklärens; mißlingt dieser, bleiben sie zwar durchaus innerhalb der Erkenntnis, sie stehen auch dann nicht mehr in limine^[1] außerhalb ihrer, wie die Abstraktion, aber sie wandern in die Versuchsgeschichte der Erkenntnis, der erkannten Irrtümer.“

– Ernst Bloch: Über Fiktion und Hypothese, 1953, in: Gesamtausgabe Bd. X, S. 21-26, S. 25

Anmerkungen

1. ↑ in limine bedeutet soetwas wie an der Schwelle

Siehe auch

• Hypothesenraum
• These, Thesenpapier
• Arbeitshypothese
• Deduktion, Abduktion
• Rhetorik, Dialektik

Literatur

• Henri Poincaré: Wissenschaft und Hypothese. Leipzig 1904.
• Karl Popper: Logik der Forschung. Wien 1935.
• Wolfgang Stegmüller: Hypothese. in: Handbuch wissenschaftstheoretischer Begriffe. Bd 2. Vandenhoeck und Ruprecht, Göttingen 1980, 284-287. ISBN 3-525-03313-3

Weblinks

---