Diffusionsbegrenztes Wachstum
- Diffusionsbegrenztes Wachstum
-
Das diffusionsbegrenzte Wachstum (diffusion limited aggregation, DLA) kommt durch zufällige Anlagerung von Teilchen zustande. Grundlage dafür ist die brownsche Molekularbewegung, nach deren Gesetzmäßigkeiten sich Teilchen in Gasen oder Flüssigkeiten thermisch bewegen. Sie bilden eines der einfachsten Mechanismen zur Erzeugung von Fraktalen.

Simulation - Anlagerung von Rußteilchen

Resultat einer DLA-Simulation
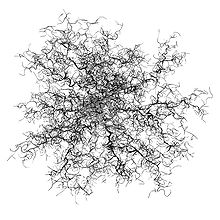
Resultat einer 3D-DLA-Simulation

Ein brownscher Baum, der in einer Kupfersulfatlösung durch elektrolytische Abscheidung entstanden ist
Die Teilchen lagern sich mit größerer Wahrscheinlichkeit an den schon bestehenden Spitzen an. Die dabei entstehenden stark verästelten Strukturen („brownsche Bäume“) sind im Grenzfall unendlich kleiner Teilchen Fraktale.
Das diffusionsbegrenzte Wachstum wurde 1981 von Leonard M. Sander und Thomas Witten beschrieben. Sie waren auf die Beobachtung solcher an Mandelbrots Fraktale erinnernde Strukturen in Ablagerungen von Eisenkolloiden aufmerksam geworden und versuchten, ihre Entstehung in einem einfachen Computermodell zu simulieren. Im Witten-Sander-Modell bewegt sich ein Teilchen überwiegend unter dem Einfluss der Diffusion (brownsche Bewegung), bis es in die Nähe eines „Clusters“ schon abgelagerter Teilchen kommt. Unterschreitet es einen Mindestabstand, lagert es an das Cluster an. Zur Überraschung von Sander und Witten ergaben sich in der Simulation verästelte, fraktale Strukturen.
Beispiele dazu:
- Anlagerung von Rußteilchen: Teilchen lagern sich an den Wänden eines Kamins an und bewirken ein Zuwachsen des Rohres
- Ausfällungen in elektrolytischen Lösungen, z.B. Kupfersulfatlösung, die man durch geeignete Kathoden zu reinem Kupfer ausfällen lässt (Siehe Bild).
- Baumartige Strukturen in der Biologie, wie Bildung der Fellzeichnungen bei Zebra, Tiger, Leopard, Tapir
- Schneeflocken, siehe auch Koch-Kurve
- Lichtenberg-Figuren
Literatur
- Thomas Witten, Leonard Sander: Diffusion limited aggregation – a kinetic critical phenomenon, Physical Review Letters, Bd. 47, 1981, S. 1400-1403
- Witten, Sander: Diffusion limited aggregation, Physical Review B, Bd. 27, 1983, S. 5686
- Witten, Sander: Fractal Growth, Scientific American, Bd.256, 1987, S.94-100
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Wachstum — Verschiedene Arten von Wachstum. Exponentielles Wachstum Lineares Wachstum … Deutsch Wikipedia
Beschränktes Wachstum — Als Wachstum bezeichnet man den zeitlichen Anstieg einer bestimmten Messgröße. Es kann daher als mathematische Ableitung einer Funktion aufgefasst werden, die zu jedem Zeitpunkt einen bestimmten Wert der Messgröße zuordnet. Das Gegenteil von… … Deutsch Wikipedia
Growth — Als Wachstum bezeichnet man den zeitlichen Anstieg einer bestimmten Messgröße. Es kann daher als mathematische Ableitung einer Funktion aufgefasst werden, die zu jedem Zeitpunkt einen bestimmten Wert der Messgröße zuordnet. Das Gegenteil von… … Deutsch Wikipedia
Zunahme — Als Wachstum bezeichnet man den zeitlichen Anstieg einer bestimmten Messgröße. Es kann daher als mathematische Ableitung einer Funktion aufgefasst werden, die zu jedem Zeitpunkt einen bestimmten Wert der Messgröße zuordnet. Das Gegenteil von… … Deutsch Wikipedia
Fraktal — Berühmtes Fraktal: die Mandelbrot Menge (sogenanntes „Apfelmännchen“) Fraktal ist ein von Benoît Mandelbrot geprägter Begriff (lateinisch fractus ‚gebrochen‘, von lateinisch frangere ‚(in Stücke zer)brechen‘), der nat … Deutsch Wikipedia
Braun'sche Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Brown'sche Bewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Brown'sche Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Brownsche Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia




