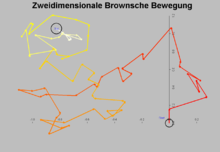
Brownsche Bewegung

Zweidimensionale brownsche Bewegung

Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen in Flüssigkeiten und Gasen bezeichnet. Dabei beschreibt jedes Atom oder Molekül eine Bewegung, deren Ausmaß temperaturabhängig ist. Weniger bekannt ist, dass bereits 1785 Jan Ingenhousz die Bewegung von Holzkohlestaub auf Alkohol beschrieb.

Brownsche Bewegung von fluoreszierenden Latex-Kügelchen (Durchmesser etwa 20nm) in Wasser mit einem SPI-Mikroskop beobachtet

Brown beobachtete unter dem Mikroskop, wie Pollen in einem Wassertropfen unregelmäßig zuckende Bewegungen machten. Ursprünglich nahm Brown an, dass dies ein Hinweis auf die Lebenskraft sei, die lange Zeit von Wissenschaftlern als existent vermutet wurde, siehe organische Chemie. Aber den Effekt konnte er schließlich auch an eindeutig unbelebten Staubkörnern beobachten. Die Erklärung dafür liefern die Moleküle des Wassertropfens, die permanent von allen Seiten gegen die größeren, sichtbaren Pollenteilchen stoßen, wie 1860 durch die maxwellsche Geschwindigkeitsverteilung mathematisch exakt beschrieben werden konnte. Dass es sich um eine Folge der Bewegung der Flüssigkeitsmoleküle und nicht anderer Ursachen handelt, bewies zuerst Christian Wiener 1863 in Experimenten.

Ein Kolloid stößt pro Sekunde etwa 10²¹-mal mit einem Lösungsmittelmolekül zusammen. Dadurch erfährt es jedes Mal eine Kraft, was zu einer zufälligen Bewegung, einem sogenannten Random Walk führt. Ohne äußere Einflüsse ist die Wahrscheinlichkeit einer Bewegungsänderung in jede Richtung gleich groß. Daher erhält man bei längerer Betrachtung für die Summe der Richtungsänderung Null.

Diffusion, Osmose und Thermophorese basieren auf dieser Bewegung der Teilchen.

Mathematisches Modell

Verwendet man den Wiener-Prozess als mathematisches Modell für die Bewegung, so kann man σ² als mittlere quadratische Verschiebung eines Teilchens pro Zeiteinheit verstehen und experimentell schätzen. Albert Einstein (1905) und Marian Smoluchowski (1906) konnten zeigen, dass $\sigma^2 = \tfrac{R T}{N_{\rm A} 3 r \pi \eta}$ gilt, wobei R die universelle Gaskonstante, T die absolute Temperatur, N_A die Avogadro-Konstante, r der Radius eines brownschen Teilchens und η die Zähigkeit (innere Reibung) der Flüssigkeit bzw. des Gases ist.^[1][2] So lässt sich die Boltzmannkonstante $k_{\rm B} = \tfrac R{N_{\rm A}}$ experimentell bestimmen. U. a. hierfür erhielt Jean Baptiste Perrin 1926 den Nobelpreis für Physik.

In der Mathematik ist eine brownsche Bewegung $B = (B_t)_{t \in [0,\infty]}$ ein zentrierter Gauß-Prozess mit Kovarianzfunktion $\mathrm{Cov}(B_t,B_s) = \mathop{\rm min}(t,s)$ für alle $t,s \geq 0$. Der resultierende stochastische Prozess ist heute zu Ehren von Norbert Wiener, der die wahrscheinlichkeitstheoretische Existenz desselben 1923 bewies, als Wiener-Prozess bekannt. Es gibt mehrere Möglichkeiten, eine brownsche Bewegung zu konstruieren:

• die abstrakte Konstruktion anhand des Schemas von Kolmogorow, wobei man dann Probleme mit der Pfadstetigkeit bekommt.
• die Lévy-Ciesielski-Konstruktion: Hierbei wird die brownsche Bewegung mit Hilfe der durch das Haarsystem auf C([0,1]) induzierten Schauderbasis bereits als stochastischer Prozess mit stetigen Pfaden konstruiert.
• Seien Z₀, Z₁, … unabhängig und standardnormalverteilt,

dann ist $S(t) = Z_0 t + \sum_{k=1}^\infty Z_k \frac{\sqrt{2} \sin(k \pi t)}{k \pi}$ eine brownsche Bewegung.

Die brownsche Bewegung spielt auch bei der Simulation von Aktienkursverläufen eine Rolle, außerdem dient sie als Grundlage der Erforschung von Warteschlangen.^[3]

Siehe auch

• Brownsche Brücke
• Gebrochene Brownsche Bewegung
• Geometrische brownsche Bewegung
• Diffusionsbegrenztes Wachstum
• Molekulare Ratsche
• Maxwellscher Dämon

Einzelnachweise

1. ↑ Einstein, A.: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen.. In: Annalen der Physik. 322, Nr. 8, 1905, S. 549–560.
2. ↑ Smoluchowski, M.: Zur kinetischen Theorie der brownschen Molekularbewegung und der Suspensionen. In: Annalen der Physik. 326, Nr. 14, 1906, S. 756–780.
3. ↑ Mathematik des Schlangestehens „Beim Warten sind wir wie Moleküle“ www.sueddeutsche.de 20. Dezember 2007, 11:11

Weblinks

• Anschauungsmaterial (www.eduhi.at)
• E. Nelson, Dynamical Theories of Brownian Motion (PDF-Datei; 465 kB)
• Java-Applet zu Brown’schen Bewegung