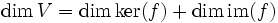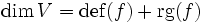Datanorm — ist ein Dateiformat für den Datenaustausch von Artikelstammdaten zwischen Produktlieferant, Fachgroßhandel und Handwerksbetrieb. Es wird vornehmlich im Baunebengewerbe in der Sanitär , Heizungs und Elektrobranche genutzt. Der Handwerker kann über … Deutsch Wikipedia
Datanorm online — DATANORM ist ein Dateiformat für den Datenaustausch von Artikelstammdaten zwischen Produktlieferant, Fachgroßhandel und Handwerksbetrieb. Es wird vornehmlich im Baunebengewerbe in der Sanitär , Heizungs und Elektrobranche genutzt. Der Handwerker… … Deutsch Wikipedia
Jordan'sche Normalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Jordan-Normalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Jordan Normalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Jordanform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Jordannormalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Jordansche Normalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Benannt wurde sie nach Marie Ennemond Camille Jordan, der sie 1871 im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme für… … Deutsch Wikipedia
Jordan’sche Normalform — Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen… … Deutsch Wikipedia
Kern-Bild-Formel — Der Rangsatz oder Dimensionssatz ist ein Satz aus dem mathematischen Teilgebiet der linearen Algebra. Er zeigt einen Zusammenhang zwischen der Dimension des Bildes und der des Kerns einer linearen Abbildung f von einem Vektorraum V in einen… … Deutsch Wikipedia
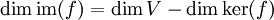 berechnen kann.
berechnen kann.