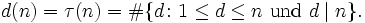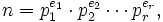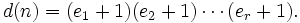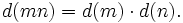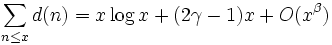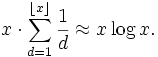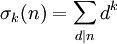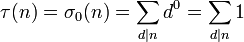Tau-Funktion

Im mathematischen Teilgebiet der Zahlentheorie gibt die Teileranzahlfunktion an, wieviele Teiler eine natürliche Zahl hat; dabei werden die Zahl selbst und die Eins mitgezählt. Die Teileranzahlfunktion wird üblicherweise mit d oder τ bezeichnet.

Definition

Für eine natürliche Zahl n ist

$d(n)=\tau(n)=\#\{d\colon 1\leq d\leq n\ \mathrm{und}\ d\mid n\}.$

Die ersten Werte sind:

n	1	2	3	4	5	6	7	8	9	10	11	12
Teiler von n	1	1, 2	1, 3	1, 2, 4	1, 5	1, 2, 3, 6	1, 7	1, 2, 4, 8	1, 3, 9	1, 2, 5, 10	1, 11	1, 2, 3, 4, 6, 12
d(n)	1	2	2	3	2	4	2	4	3	4	2	6

Eigenschaften

• Hat die Zahl n die Primfaktorzerlegung

$n=p_1^{e_1}\cdot p_2^{e_2}\cdots p_r^{e_r},$

so gilt^[1]

$d(n) = (e_1+1)(e_2+1)\cdots(e_r+1).$

• Insbesondere gilt für teilerfremde Zahlen m und n:

$d(mn) = d(m)\cdot d(n).$

Aufgrund dieser Eigenschaft bezeichnet man die Teileranzahlfunktion als (multiplikative) zahlentheoretische Funktion.

• Eine Zahl n ist genau dann eine Primzahl, wenn d(n) = 2 ist.
• Eine Zahl n ist genau dann eine Quadratzahl, wenn d(n) ungerade ist.
• Die zur Teileranzahlfunktion gehörige Dirichlet-Reihe ist das Quadrat der riemannschen Zetafunktion:^[2]

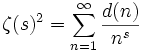$\zeta(s)^2=\sum_{n=1}^\infty\frac{d(n)}{n^s}$ (für $\operatorname{Re}\,s>1$).

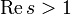Asymptotik

Im Mittel ist 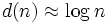$d(n)\approx\log n$, präziser: Es gibt Konstanten 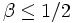$\beta\leq1/2$, so dass^[3]

$\sum_{n\leq x}d(n)=x\log x+(2\gamma-1)x+O(x^\beta)$

gilt. (Dabei sind „O“ ein Landau-Symbol und γ die Euler-Mascheroni-Konstante.)

Als Heuristik kann die Erkenntnis dienen, dass eine Zahl 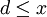$d\leq x$ ein Teiler von etwa 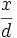$\frac xd$ Zahlen 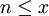$n\leq x$ ist, damit wird die Summe auf der linken Seite in etwa zu

$x\cdot\sum_{d=1}^{\lfloor x\rfloor}\frac 1d\approx x\log x.$

(Zum letzten Schritt siehe harmonische Reihe.)

Der Wert β = 1 / 2 wurde bereits von P. G. L. Dirichlet bewiesen;^[4] die Suche nach besseren Werten ist deshalb auch als dirichletsches Teilerproblem bekannt.

Bessere Werte wurden von G. F. Woronoi (1903, x^{1 / 3}logx)^[5] und J. van der Corput (1922, β = 33 / 100)^[6] angegeben. Auf der anderen Seite zeigten G. H. Hardy und E. Landau, dass 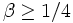$\beta\geq1/4$ gelten muss.^[7] Die möglichen Werte für β sind immer noch Forschungsgegenstand.

Verallgemeinerungen

Die Teilerfunktion σ_k(n) ordnet jeder Zahl n die Summe der k-ten Potenzen ihrer Teiler zu.^[8]

$\sigma_k(n) = \sum_{d\mid n} d^k$

Die Teileranzahlfunktion ist der Spezialfall der Teilerfunktion für k = 0.

$\tau(n) = \sigma_0(n) = \sum_{d\mid n} d^0 = \sum_{d\mid n} 1$

Literatur

• G. H. Hardy, E. M. Wright, An Introduction to the Theory of Numbers, 4. Auflage, Oxford University Press, Oxford 1975. ISBN 0-19-853310-1

Quellen

1. ↑ Hardy-Wright, a.a.O., Theorem 273, S. 239
2. ↑ Hardy-Wright, a.a.O., Theorem 289, S. 250
3. ↑ Hardy-Wright, a.a.O., Theorem 320, S. 264
4. ↑ P. G. L. Dirichlet, Über die Bestimmung der mittleren Werthe in der Zahlentheorie, Abhandlungen der Königlich Preussischen Akademie der Wissenschaften von 1849, S. 69–83; oder Werke, Band II, S. 49–66
5. ↑ G. Voronoï, Sur un problème du calcul des fonctions asymptotiques, J. Reine Angew. Math. 126 (1903) 241–282
6. ↑ J. G. van der Corput, Verschärfung der Abschätzung beim Teilerproblem, Math. Ann. 87 (1922) 39–65. Berichtigungen 89 (1923) 160.
7. ↑ G. H. Hardy, On Dirichlet's divisor problem, Lond. M. S. Proc. (2) 15 (1915) 1–25. Vgl. Hardy-Wright, a.a.O., S. 272
8. ↑ Eric W. Weisstein: Divisor Function auf MathWorld (englisch)